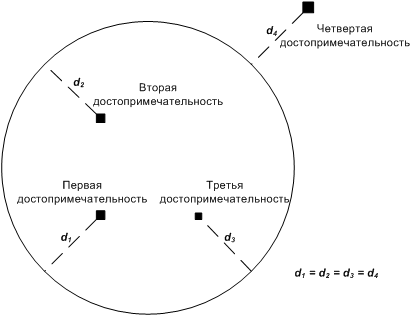
В наши дни предоставление поверхностей заборов и стен промышленных зданий рекламодателям — уже не оригинальный способ получить дополнительный заработок, а нечто само собой разумеющееся.
Небольшая компания «Домострой» также решила выйти на этот рынок и стала предлагать место для рекламы на своих блоках заборов. Блок представляет собой параллелепипед размером \(1\times1\times L\), на одной из сторон которого есть место для рекламы — пространство
размера \(1\times L\), в которое можно вписать ровно \(L\) букв латинского алфавита.
К сожалению, иногда сделки у компании срывались, и заранее подготовленные блоки с рекламой отправлялись на склад. Со временем там скопилось приличное количество блоков различных типов (блоки разных типов отличаются друг от друга только надписью), поэтому
было решено использовать их вторично.
Была предложена следующая идея: если поставить несколько блоков друг на друга и закрасить ненужные буквы, то, читая сверху вниз и слева направо, можно будет прочитать какой-нибудь другой текст, как показано на рисунке.
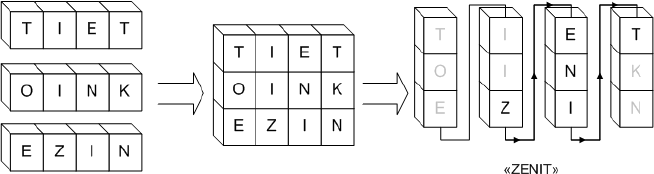
Таким образом, можно получить рекламную надпись для нового клиента. При этом из эстетических соображений при прочтении конечной надписи разрывы в виде закрашенных букв недопустимы.
После того, как некоторое число \(K\) блоков, каждый из которых имеет длину \(L\), поставили друг на друга, получилась прямоугольная таблица размером \(K\times L\), в каждой клетке которой находится буква латинского алфавита. Каждый рекламный блок соответствует
строке этой таблицы. Теперь содержимое этой таблицы выписывается по столбцам, начиная с самого левого. При этом в каждом столбце буквы выписываются сверху вниз. В случае, изображённом на рисунке, в результате этого процесса получилась бы строка
«TOEIIZENITKN». Необходимо, чтобы рекламная надпись, требуемая заказчику, входила в получившуюся строку как подстрока «TOEIIZENITKN».
Требуется написать программу, которая будет определять, какое минимальное количество блоков надо использовать, чтобы получить рекламную надпись, необходимую заказчику. При этом можно считать, что на складе блоков каждого типа неограниченно много.
Выходные данные
В первой строке выходного файла необходимо вывести натуральное число \(K\) — минимальное количество блоков, которое нужно использовать для составления новой рекламы. Следующая строка должна содержать \(K\) чисел — номера типов блоков, которые нужно для
этого использовать, перечисляя их сверху вниз. Типы блоков нумеруются с единицы в порядке их задания во входном файле.
Если ответов несколько, выведите любой из них. Если решения не существует, выведите в выходной файл число \(-1\).