Теоретический материал

ДП по изломанному профилю

Другое название этому методу -- "быстрая динамика по профилю". Идея в том, чтобы добиться как можно меньшего числа переходов (от одного профиля к другому).

Рисунок 5: Изображение профиля $ \langle$33, 2$ \rangle$  ( 33 = 20 + 25).
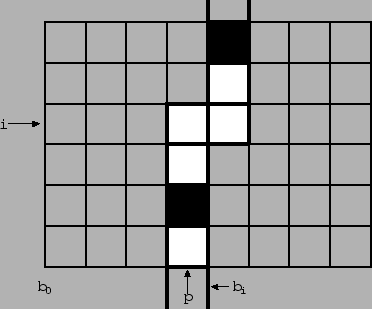
\begin{figure}\centering { \epsfbox{dprof/pic.3} } \end{figure}

Еще раз используем в качестве примера задачу о замощении. Базовая линия теперь будет ломаной: при прохождении через i-ю горизонталь сверху вниз, она переходит на предыдущую вертикаль и спускается до низу (см. рис. 5).

Профилем будет пара $ \langle$p, i$ \rangle$, в p будет информация о n + 1 маленьком квадратике слева от базовой линии, имеющем с ней общие точки; i обозначает номер горизонтали, на которой произошел излом. Квадратики профиля будут нумероваться сверху вниз, так что угловой будет иметь номер i + 1. Горизонтали будем нумеровать нуля, так что i пробегает значения 0..n - 1.

Для двух профилей pr1 = $ \langle$p1, i1$ \rangle$ и pr2 = $ \langle$p2, i2$ \rangle$ положим d[pr1][pr2] = 1 если и только если:

а)
если i < n - 1, то i1 + 1 = i2; иначе i2 = 0;
б)
можно так положить доминошку, накрывающую (i + 1)-й квадратик, что после этого в p2 будет храниться в точности информация о соответствующих квадратиках.

Проще говоря, доминошку можно класть только двумя способами -- как показано на рисунках (на (i + 1)-й квадратик можно положить не более одной вертикальной и горизонтальной доминошки). То, что потом получается после сдвига вниз излома, и будет новым профилем. Заметим, что если (i + 1)-я клетка занята, то доминошку уже не надо класть, и $ \langle$p, i$ \rangle$ логично отождествить с $ \langle$p, i + 1$ \rangle$ ("i + 1" пишется условно, нужно всегда иметь в виду возможность i = n - 1).

Легко заметить, что количество профилей увеличилось в 2n раз (добавилось число от 1 до n и еще один бит). Но зато количество переходов резко сократолсь с 2n до двух!

В нижеприведенном куске кода для профиля $ \langle$p, i$ \rangle$ выводятся все переходы из него (напомним, что нумерация горизонталей начинается с нуля и i = 0..n - 1): 

procedure print_all_links(p, i : integer);
begin
    if (bit(p, i + 1) = 0) then begin
        if (i = n - 1) then begin
            writeln('<', (p - (2 shl i)) shl 1, ', ', 0, '>');
        end else begin
            writeln('<', p - (2 shl i), ', ', i + 1, '>');
        end;
    end else begin
        if (bit(p, i) = 0) then begin
            if (i = n - 1) then begin
                writeln('<', p shl 1, ', ', 0, '>');
            end else begin  writeln('<', p + (1 shl i), ', ', 
                            (i + 1) mod n, '>');         end;
        end;
        if (i < n - 1) and (bit(p , i + 2) = 0) then begin
            writeln('<', p + (4 shl i), ', ', i + 1, '>');
        end;
    end;
end;

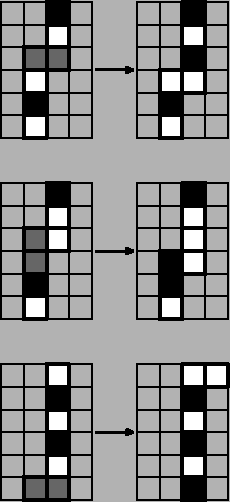
\epsfbox{dprof/pic.4}

Рисунок 6. Возможные переходы.

При такой реализации существует немало профилей только с одним переходом (например, у которых (i + 1)-й бит равен единице).

Отождествим все профили с один переходом с теми, кто их них получается. Это будет выглядеть так: пусть pr2 (и только он) получается из pr1, который, в свою очередь, получается из pr0. Тогда имеются такие соотношения: d[pr0, pr1]=1, d[pr1, pr2]=1. Отождествить pr1 и pr2 -- это, по сути, заменить эти два соотношение на одно, то есть теперь d[pr0, pr1]=0 и d[pr1, pr2]=0, но d[pr0, pr2]=1, и так далее.

Таким образом, возможно сокращение профилей не менее чем вдвое. Дальнейшие оптимизации мы оставляем читателю.

В итоге получаем асимптотику 2nn (количество переходов, то есть время на вычисление a[i]) умножить на m равно O(2nnm). Она значительно лучше всего, что мы получали до сих пор, и это серьезный повод использовать изломанный профиль вместо обычного.