Теоретический материал
XVIII Всероссийская олимпиада школьников по информатике
Первый тур, Кисловодск, 23 апреля 2006 года
Задача 2. Файловый менеджер
Общий шаг алгоритма – k раз находить кратчайшие пути из одной вершины в другую на предварительно построенном графе.
Будем называть имена файлов строками.
Рассмотрим полный ориентированный граф с N вершинами, где вершина i соответствует файлу номер i. Вес ребра (i, j) – минимальная стоимость добраться из позиции курсора номер i в позицию j, используя только одну возможность менеджера (нажать клавишу вверх, нажать клавишу вниз, нажать клавишу Alt и последовательность символов). Ребра, реализующие первые две возможности (up, down), соединяют все вершины, номера которых отличаются на 1. Вес таких ребер равен 1.
Самая главная сложность этой задачи состоит в том, чтобы быстро найти веса ребер для последней возможности (Alt + <Text>). Вес такого ребра (i, j) – минимальная длина последовательности нажатий клавиш, которая переводит курсор с i-го файла на j-й. Если из i в j нельзя попасть только с помощью “Alt”, то вес ребра будет плюс бесконечность.
Таким образом, чтобы найти последовательность нажатий минимальной длины, перемещающую курсор из позиции A в позицию B, надо найти кратчайший путь из A в B в нашем графе.
Если запустить алгоритм Дейкстры из вершины A, то в d[B] получим искомую длину.
Пусть мы знаем, как быстро вычислять массив common[i][j] = максимальный общий префикс строк номер i и j. Тогда d[i][j] – вес ребра (i, j) – равен максимуму среди (common[t][j] + 2) i <=t < j (если i > j, то t пробегает значения i, i + 1, …N, 1, …, j – 1). Это верно, так как надо нажать сначала Alt, потом max(common[t][j]) букв, потом еще одну. Если нажать менее чем d[i][j] клавиш, то курсор попадет на какую-нибудь строку между i и j. Если d[i][j] получилось больше, чем длина j-го слова + 1, то из i в j нельзя попасть только с помощью “Alt”, d[i][j] присваиваем плюс бесконечность.
Например, для набора
aaa
baa
aa
bbbb
bbcc
d[1][5] = 4, d[1][3] = +∞.
Вычисление D по common несложно реализовать за O(N2) следующим образом:
d[j – 1][j] = common[j – 1][j] + 2,
d[j – 2][j] = max(common[j – 2][j] + 2, d[j – 1][j]),
…
d[i][j] = max(common[i][j] + 2, d[i + 1][j]).
Обсудим три способа найти common[i][j] для всех i, j.
а) O(N*log(N)*L), где L – максимальная длина слов.
Отсортируем все имена в лексикографическом порядке, пусть строка i имеет номер P(i) в отсортированном списке.
Найдем c[P(i)] – размер наибольшего общего префикса строк P(i), P(i + 1). Тогда common[i][j], где
P(i) < P(j) – минимум среди всех c[t], P(i) ≤ t < P(j). Действительно, если P(i) и P(j) имеют общий префикс длиной L, то c[t] ≥ L, причем должно быть хотя бы одно равенство.
Тогда
common[P(j – 1)][P(j)] = c[P(j – 1)],
common[P(j – 2)][P(j)] = max(c[j – 2], common[P(j – 1)][P(j)]),
…
common[P(i)][P(j)] = max(c[P(i)], common[P(i + 1)][P(j)]).
б) O(N2 + N*L) (предложено одним из участников)
Будем искать common методом динамического программирования.
Пусть B[i + 1][j] – такое 1 ≤t ≤ j, что common[i + 1][t] максимально.
Допустим, вычислены все common[a][b] и B[a][b], a ≤ i, b ≤ i. Научимся находить common[i + 1][j + 1] и
B[i + 1][j + 1] при условии, что для всех пар (i + 1, t), t ≤ j, все уже вычислено. Возьмем A = B[i + 1][j]. Тогда первые min(common[i + 1][A], common[A][j + 1]) символов у строк (i + 1) и (j + 1) совпадают. Тогда если
common[j + 1][A] < common[i + 1][A], то
common[i + 1][j + 1] = common[j + 1][A] и
B[i + 1][j + 1] = A.
В противном случае находим common[i + 1][j + 1] непосредственно сравнивая символы с номерами common[i + 1][A] + 1, …, L у строк (i + 1), (j + 1), пока не найдется несовпадения. При этом
B[i + 1][j + 1] = max(common[i + 1][j + 1], B[i + 1][j]).
Таким образом, для каждого (i + 1) непосредственных сравнений будет не более L, остальных действий O(N), так что заявленная оценка верна.
в) O(S + N2), где S – суммарная длина всех имен файлов.
Допишем к концу каждого имени файла символ “$”. Построим сжатый бор из таких расширенных строк (подробнее о борах см. [1]). Тогда каждой строке будет соответствовать лист в боре (у которого путевая метка равна расширенной строке). В противном случае получим, что префиксом какой-то строки A будет S$, где S – строка без листа, тогда A = S, чего не может быть по условию.
Тогда common[i][j] - длина путевой метки наименьшего общего предка для пары листьев, соответствующих строкам i, j (обозначается LCA(i, j)).
Вспомним, как алгоритм поиска в глубину раскрашивает вершины в процессе работы: вначале все вершины белые; когда вершина только начинает обрабатываться, ее красят в серый цвет; после того, как все ее сыновья (или вершины, в которые из нее ведут ребра) станут черными (обработанными), она становится черной.
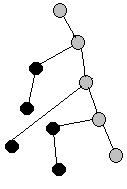
Предложение. Пусть вершину j только что перекрасили в серый цвет (это значит, что все ее сыновья еще белые). Тогда LCA(i, j) для любой черной i будет q(i) - наиболее удаленная от корня серая вершиной, являющейся предком i.
Так как конфигурация серых и черных вершин меняется по ходу выполнения алгоритма, то будем различать q(i) для разных моментов времени (в частности, когда i не является черной, q(i) не определена).
Итак, будем обходить в глубину из корня наш бор как дерево. В массиве q[i] в любой момент времени будет храниться q(A) в текущий момент времени, где A – лист, соответствующий строке i. Также будет храниться список листьев, уже ставших черными. Тогда при перекрашивании очередного листа в серый цвет надо пробежаться по списку уже черных и проставить соответствующие значения common. При перекрашивании листа в черный цвет надо добавить его в список черных. Если при обработке любой вершины u оказывается, что q[i] для какого-то i ссылается на черную вершину, то q[i] – значение q(A) для предыдущего момента времени, и q[i] надо изменить на u.
Подробнее об алгоритме поиска LCA см. [2] среди задач к разделу «Обход в глубину».
Литература.
[1]. Дэн Гасфилд. «Строки, деревья и последовательности в алгоритмах. Информатика и вычислительная биология»
[2]. Кормен, Лейзерсон, Ривест. «Алгоритмы: построение и анализ»