Описание структуры

На практике дерево Фенвика представляет собой массив B из N чисел: B₀, B₁, ..., B_{N - 1}, в k-м элементе которого хранится сумма элементов массива A с f (k)-го по k-й: B_k = A_i, где f (k) = k& (k + 1). Под & имеется ввиду операция побитового И.

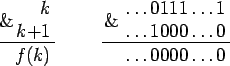
Рис. 1.

Рассмотрим двоичное представление числа k (рис. 1): пусть в нем сначала идет произвольная последовательность 0 и 1, потом 0 и дальше некоторое количество единиц, в том числе нулевое. f (k) получается из k заменой всех этих подряд идущих единиц в младших разрядах нулями. Если же в младшем разряде числа k стоит 0, то f (k) = k. Так, например, для k = 11₁₀ = 1011₂ получаем f (k) = 1000₂ = 8₁₀, а для k = 10₁₀ = 1010₂ получаем f (k) = 1010₂ = 10₁₀. Отметим важное свойство функции f: 0f (k)k для любого k 0.

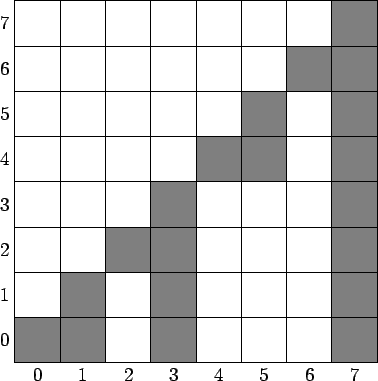
Рис. 2.

Диаграмма на рис. 2 показывает, что будет храниться в массиве B (дереве Фенвика) при N = 8: клетка i-й строки k-го столбца заштрихована, если A_i входит в частичную сумму B_k, то есть f (k)ik.

Рассмотрим, как с помощью дерева Фенвика реализуются операции ответа на запрос rsq(i, j) о частичной сумме элементов массива A с i-го по j-й и запрос update(k, d ) прибавления к k-му элементу массива A числа d.