Теоретический материал

Ответ на запрос о частичной сумме элементов массива A -- rsq(i, j)

Заметим, что rsq(i, j) = rsq(0, j) - rsq(0, i - 1) (для i = 0 положим rsq(0, - 1) = 0). Таким образом, для ответа на запрос rsq(i, j) достаточно научиться отвечать на запрос вида rsq(0, k), который для краткости обозначим rsq(k).

Ответ на запрос rsq(k) вычисляется следующим образом:

rsq(k) = B_k + B_{f(k) - 1} + B_{f(f(k) - 1) - 1} +...+ B_{f(f(...f(k) - 1...) - 1) - 1}

Перепишем эту формулу в виде

rsq(k) = B_k₀ + B_k₁ + B_k₂ +...+ B_{k_n}

-- суммирование начинается с B_k, а индекс каждого следующего слагаемого получается из индекса предыдущего по формуле: k_{i + 1} = f (k_i) - 1 = (k_i& (k_i + 1)) - 1, где k₀ = k. Суммирование заканчивается, когда k_i становится меньше 0, то есть k_{m + 1} = f (k_m) - 1 < 0. Такой момент наступает, поскольку k_{i + 1} = f (k_i) - 1 $\le$ k_i - 1 < k_i, то есть каждый следующий индекс строго меньше предыдущего.

Покажем, почему указанная сумма ([*]) действительно будет являться ответом на запрос rsq(k), то есть B_k₀ + B_k₁ + B_k₂ +...+ B_{k_n} = $\displaystyle \sum_{i=0}^{k}$ A_i.

Действительно,

B_k₀ + B_k₁ + B_k₂ +...+ B_{k_n} =
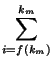= $\displaystyle \sum_{i=f(k_0)}^{k_0}$ A_i + $\displaystyle \sum_{i=f(k_1)}^{k_1}$ A_i + $\displaystyle \sum_{i=f(k_2)}^{k_2}$ A_i +...+ $\displaystyle \sum_{i=f(k_m)}^{k_m}$ A_i =
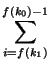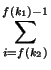= $\displaystyle \sum_{i=f(k_0)}^{k_0}$ A_i + $\displaystyle \sum_{i=f(k_1)}^{f(k_0)-1}$ A_i + $\displaystyle \sum_{i=f(k_2)}^{f(k_1)-1}$ A_i +...+ $\displaystyle \sum_{i=f(k_m)}^{f(k_{m-1})-1}$ A_i =
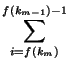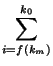= $\displaystyle \sum_{i=f(k_m)}^{k_0}$ A_i.

Для последнего индекса k_m верно: f (k_m) - 1 < 0, откуда в силу неотрицательности f (k_m) следует f (k_m) = 0, то есть 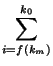$\displaystyle \sum_{i=f(k_m)}^{k_0}$ A_i = $\displaystyle \sum_{i=0}^{k}$ A_i. Таким образом, указанная сумма ([*]) и будет суммой всех элементов массива A с 0-го по k-й.

Например, для k = 14 по формуле ([*]) имеем:

rsq(14) = B₁₄ + B₁₃ + B₁₁ + B₇ =
= $\displaystyle \sum_{i=14}^{14}$ A_i + $\displaystyle \sum_{i=12}^{13}$ A_i + $\displaystyle \sum_{i=8}^{11}$ A_i + $\displaystyle \sum_{i=0}^{7}$ A_i = $\displaystyle \sum_{i=0}^{14}$ A_i.

Ниже приводится текст подпрограммы, реализующий ответ на запрос rsq(k):

 1: Function rsq(k : LongInt) : LongInt;
 2: var 
 3: res : LongInt; 
 4: begin 
 5: res := 0; 
 6: while (k >= 0) do begin 
 7: inc(res, B[k]); 
 8: k := k and (k + 1) - 1; 
 9: end; 
10: rsq := res; 
11: end;

k₀	14	1110₂
f (k₀)	14	1110₂
k₁	13	1101₂
f (k₁)	12	1100₂
k₂	11	1001₂
f (k₂)	8	1000₂
k₃	7	0111₂
f (k₃)	0	000₂

Рис. 3.

Для оценки времени работы данной подпрограммы необходимо оценить количество итераций цикла while в строках 6-9, то есть количество слагаемых m в сумме ([*]). Для этого рассмотрим двоичное представление числа k и то, как оно преобразуется при вычислении номера следующего индекса суммы по предыдущему: k_{i + 1} = f (k_i) - 1, где k₀ = k.

Сделаем это на примере для k = 14 (рис. 3). Количество слагаемых равно количеству единичных битов в числе f (k) плюс один. Переход к каждому следующему индексу «выбивает» ровно по одному единичному биту из числа f (k_i). А поскольку в худшем случае количество единичных бит в f (k) может быть порядка O(log N), то и ответ на запрос rsq(k) в худшем случае требует порядка O(log N) времени.