Теоретический материал

Изменение k-го элемента массива A -- update(k, d )

При изменении k-го элемента массива A необходимо соответствующим образом изменить элементы массива B, в определении которых частичные суммы содержат элемент A_k. То есть для выполнения операции update(k, d ) (прибавления к k-му элементу массива A числа d) нужно прибавить d к тем элементам B_j массива B, для которых f (j) $\le$ k $\le$ j.

Утверждается, что все такие j, и только они, являются элементами последовательности k₀, k₁, k₂, ..., k_m, где k₀ = k, k_{i + 1} = k_i | (k_i + 1), k_{m + 1} = k_m | (k_m + 1) > N - 1. Под | имеется в виду операция побитового ИЛИ.

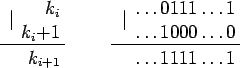
$\epsfbox{fenwick/fenwick04.eps}$

Рис. 4.

Сначала покажем, что указанная последовательность строго возрастает, и ее длина составляет порядка O(log N) в худшем случае. Для этого рассмотрим двоичное представление числа k_i (рис. 4). Число k_{i + 1} получается из k_i заменой младшего нулевого бита на единичный. Таким образом, k_{i + 1} > k_i, а длина последовательности m заведомо не превосходит количества бит в двоичном представлении числа N.

N - 1	92	1011100₂
k₀ = k	73	1001001₂
k₁	75	1001011₂
k₂=k_m	79	1001111₂
k₃	95	1011111₂

Рис. 5.

На рис. 5 приведен пример указанной последовательности для N = 93 и k = 73.

Покажем, почему элементы последовательности являются индексами тех и только тех элементов массива B, которые нужно изменить при операции update(k, d ).

j	X0... k
k	Y1... k

Рис. 6.

Поскольку при увеличении номера элемента последовательности, количество единичных битов на конце k_i возрастает, то f (k_i) убывает. Учитывая еще и то, что сама последовательность k_i возрастает, получаем:

f (k_m) <...< f (k₂) < f (k₁) < f (k₀) $\displaystyle \le$ k = k₀ < k₁ < k₂ <...< k_m

Таким образом, все элементы нашей последовательности являются индексами тех элементов массива B, которые надо изменить.

Покажем, что других элементов, которые надо изменить, нет. Предположим, что есть некоторый индекс j, не лежащий в нашей последовательности, такой что f (j) $\le$ k $\le$ j.

Рассмотрим младший бит, в котором у j стоит 0, а у k стоит 1 -- такой существует, поскольку j не встречается в последовательности k_i. Обозначим числа, образованные более старшими битами чисел j и k, через X и Y соответственно. Если X > Y, то j $\ge$ f (j) $\ge$ X0...0₂ > k, а стало быть, частичная сумма B_j не содержит элемента A_k. Если же X $\le$ Y, то k > j $\ge$ f (j) и опять же частичная сумма B_j не содержит элемента A_k. Значит, индексы всех элементов массива B, которые надо изменить присутствуют в последовательности k_i.

Ниже приводится текст подпрограммы, реализующий операцию изменения update(k, d):

 1: Procedure update(k, d : LongInt);
 2: begin
 3: while (k < N) do begin
 4: inc(B[k], d);
 5: k := k or (k + 1);
 6: end;
 7: end;

В силу того, что длина последовательности k_i составляет O(log N) в худшем случае, количество итераций цикла while в строках 3-6, а значит, и время работы процедуры update(k, d), составляет O(log N).