Теоретический материал
Обобщение на двумерный случай
Оказывается, что дерево Фенвика достаточно легко обобщается на двумерный (а вообще говоря, и на k-мерный) случай.
Пусть задан двумерный массив A размера M×N, элементами которого являются числа Aij, 0![]() i
i![]() M - 1, 0
M - 1, 0![]() j
j![]() N - 1. Двумерное дерево Фенвика -- это структура данных, позволяющая выполнять две операции:
N - 1. Двумерное дерево Фенвика -- это структура данных, позволяющая выполнять две операции:
- rsq(x1, y1, x2, y2) -- выдать сумму
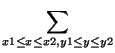 Axy элементов Axy на прямоугольнике x1
Axy элементов Axy на прямоугольнике x1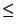 x
x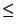 x2, y1
x2, y1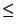 y
y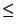 y2;
y2; - update(x, y, d ) -- прибавить к элементу Axy некоторое число d.
Двумерное дерево Фенвика представляет собой двумерный массив B размера M×N, элементами которого являются числа Bxy, 0![]() x
x![]() M - 1, 0
M - 1, 0![]() y
y![]() N - 1. Bxy =
N - 1. Bxy = 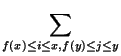 Aij.
Aij.
По аналогии с одномерным случаем заметим (рис. 7), что
- rsq(0, 0, x2, y1-1) + rsq(0, 0, x1-1, y1-1).
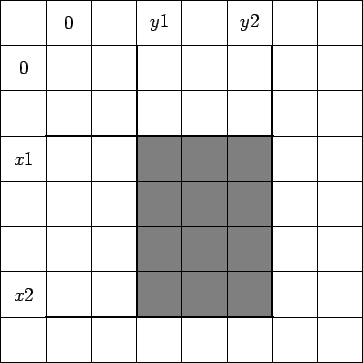
Рис. 7.
Таким образом, для ответа на запрос rsq(x1, y1, x2, y2) достаточно научиться отвечать на запросы вида rsq(0, 0, x, y), которые для краткости обозначим rsq(x, y).
В остальном, реализация операций rsq(x, y) и update(x, y, d ) делается аналогично одномерному случаю из соображений независимости по каждому направлению.
Ниже приводится текст подпрограмм, реализующих операции rsq(x, y) и update(x, y, d ):
1: Function rsq(x, y : LongInt) : LongInt;
2: var
3: i,res : LongInt;
4: begin
5: res := 0;
6: while (x >= 0) do begin
7: i := y;
8: while (i >= 0) do begin
9: inc(res, B[x, i]);
10: i := i and (i + 1) - 1;
11: end;
12: x := x and (x + 1) - 1;
13: end;
14: rsq := res;
15: end;
1: Procedure update(x, y, d : LongInt);
2: var
3: i : LongInt;
4: begin
5: while (x < M) do begin
6: i := y;
7: while (i < N) do begin
8: inc(B[x, i], d);
9: i := i or (i + 1);
10: end;
11: x := x or (x + 1);
12: end;
13: end;
По соображениям, аналогичным тем, что приводились в одномерном случае, времена работы rsq(x, y) и update(x, y, d ) составляют O((log M)(log N)) и O((log M)(log N)) соответственно.
Для построения двумерного дерева Фенвика достаточно взять изначально нулевой массив B и M×N раз применить операцию update: update(x, y, Axy), 0![]() x
x![]() M - 1, 0
M - 1, 0![]() y
y![]() N - 1. Построение двумерного дерева Фенвика требует O(MN(log M)(log N)) времени и O(MN) памяти.
N - 1. Построение двумерного дерева Фенвика требует O(MN(log M)(log N)) времени и O(MN) памяти.