Теоретический материал

Некоторые обозначения и определения

Матрицей размера n×m называется прямоугольная таблица n×m, составленная из чисел.

Обычно матрицы обозначают заглавными латинскими буквами. Элемент i-й строки j-го столбца матрицы A обозначают через aij или a[i, j] (соответствующая маленькая латинская буква с индексами).

Произведением двух матриц $ {A \atop n \times m}$ и $ {B \atop m \times k}$ называется матрица такая $ {C \atop n \times k}$, что

cij = $\displaystyle \sum_{t = 1}^{m}$aitbtj. (1)

В этом случае пишут: C = AB.

D в степени k (Dk), при условии, что D -- квадратная (т. е. n = m) определяется следующим образом:

  • D0 = E (единичная матрица), где

    E = $\displaystyle \left(\vphantom{\begin{array}{ccccccccc} 1 & 0 & 0 & \ldots & 0 \... ...dots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \end{array}}\right.$$\displaystyle \begin{array}{ccccccccc} 1 & 0 & 0 & \ldots & 0 \\ 0 & 1 & 0 & ... ...ots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \end{array}$$\displaystyle \left.\vphantom{\begin{array}{ccccccccc} 1 & 0 & 0 & \ldots & 0 \... ...dots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \end{array}}\right)$.

    На диагонали у нее стоят единицы, в остальных клетках -- нули. Она не зря называется единичной -- при умножении на нее матрица не изменяется: AE = EA = A.

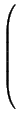
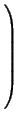  • Di = Di - 1D, i > 0.

В приводимом коде будет использоваться функция bit(x,i), возвращающая единицу или ноль -- i-й бит в двоичной записи числа x (нумерация битов с нуля). 

// возвращает i-й бит числа x, нумерация с нуля
function bit(x, i : integer) : integer;
begin
    if (i < 0) then bit := 0 else
        if (x and (1 shl i) = 0) then bit := 0 else bit := 1;
end;