Теоретический материал

Задача о симпатичных узорах

Рассмотрим еще одну задачу с прямоугольной таблицей.

Дана таблица n×m, каждая клетка которой может быть окрашена в один из двух цветов: белый или черный. Симпатичным узором называется такая раскраска, при которой не существует квадрата 2×2, в котором все клетки одного цвета. Даны n и m. Требуется найти количество симпатичных узоров для соответствующей таблицы.

Рисунок 3: Первые два узора симпатичные; у третьего и четвертого есть полностью черный и, соответственно, белый квадратик 2×2.
\begin{figure}\centering { \epsfbox{dprof/pic.5}} \end{figure}

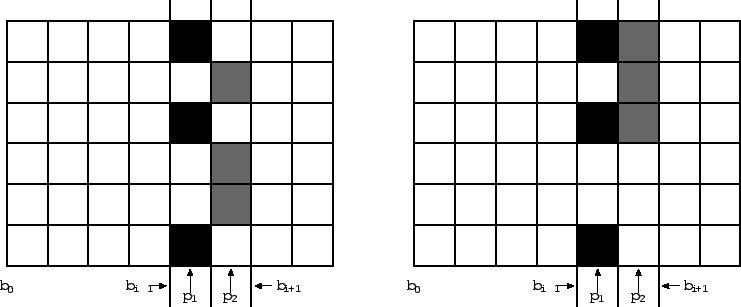
Будем считать профилем для bi битовую карту i-го столбца (единицей будет кодировать черную клетку, а нулем -- белую). При этом узор, заключенный между нулевой и i-й базовыми линиями, является симпатичным.

Из профиля p1 для bi можно получить p2 для bi + 1, если и только если можно так закрасить (i + 1)-й столбец, что его битовая карта будет соответствовать p2, и между bi - 1 и bi + 1 не будет полностью черных либо белых квадратиков 2×2.

Рисунок 4: На левом рисунке p1 = 1 + 4 + 32 = 37, p2 = 2 + 8 + 16 = 26; так как между bi - 1 и bi + 1 не встречаются одноцветные квадратики 2×2, то p2 может быть получен из p1. На рисунке справа p1 также равно 37, а p2 = 1 + 2 + 4 = 7.
\begin{figure}\centering { \epsfbox{dprof/pic.6} } \end{figure}

Сколькими же способами из одного профиля можно получить другой? Понятно, что закрасить нужным образом либо можно, либо нельзя (так как раскрашивать можно единственным образом -- так, как закодировано в p2). Таким образом, d[p1, p2] $ \in$ {0, 1}.

Вычислять D можно либо проверяя на "совместимость" (то есть наличие одноцветных квадратов 2×2) все пары профилей, либо генерируя все допустимые профили для данного. Ниже приведен код, реализующий первую идею: 

// можно ли из p1 получить p2
function can(p1, p2 : integer) : boolean;
var i : integer;
    b : arrray[1..4] of byte;
begin
    for i := 0 to n - 2 do begin
        b[1] := bit(p1, i);
        b[2] := bit(p1, i + 1);
        b[3] := bit(p2, i);
        b[4] := bit(p2, i + 1);

        if (b[1] = 1) and (b[2] = 1) and (b[3] = 1) 
                               and (b[4] = 1) then begin
            // квадрат в строках i и i + 1 черный
            can := false;
            exit;
        end;

        if (b[1] = 0) and (b[2] = 0) and (b[3] = 0) 
                               and (b[4] = 0) then begin
            // квадрат в строках i и i + 1 белый
            can := false;
            exit;
        end;
    end;
    can := true;    
end;

procedure determine_D;
var p1, p2 : integer;
begin
    for p1 := 0 to (1 shl n) - 1 do
        for p2 := 0 to (1 shl n) - 1 do
            if can(p1, p2) then d[p1, p2] :=1
            else d[p1, p2] := 0;
end;

После того, как вычислена матрица D, остается просто применить формулу (2) (так как расуждения на этом этапе не изменяются).