Динамическое программирование

Рекуррентное соотношение (2) будет встречаться нам не только в задаче о замощении или симпатичном узоре, но и во многих других задачах, решаемых динамикой по профилю. Поэтому логично, что существует несколько способов вычисления A, используя уже вычисленную D (а не только наивно пo (2)). В этом пункте мы рассмотрим способ, основанный на возведении в степень матрицы:

1)

a[i] можно считать матрицей 1×2ⁿ;

2)

D -- матрица 2ⁿ×2ⁿ;

3)

a[i] = a[i - 1]D. Если расписать эту формулу по определению произведения, то получится в точности (2).

Следуя определению степени матрицы, получаем

Вспомним, как возвести действительное число a в натуральную степень b за O(log b) (считaем, что два числа перемножаются за O(1)). Представим b в двоичной системе счисления: b = 2^i₁ + 2^i₂ +...+ 2^i_k, где i₁ < i₂ <...< i_k. Тогда k = O(log b). Заметим, что a²ⁱ получается из a^{2(i - 1)} возведением последнего в квадрат. Таким образом, за O(k) можно вычислить все a^p_t, p_t = 2^i_t, t = 1, ..., k. Перемножить их за линейное время тоже не представляет труда.

Логично предположить, что аналогичный алгоритм сгодится и для квадратных матриц. Единственное нетривиальное утверждение -- A²ⁱ = (A^{2i - 1})², ведь по определению A^2t = 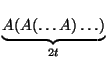, а мы хотим приравнять его к (A^t)(A^t). Его истинность следует из ассоциативности умножения матриц (AB)C = A(BC). Само свойство можно доказать непосредственно, раскрыв скобки в обеих частях равенства.

Приведем код процедуры возведения в степень (функция mul перемножает две квадратные матрицы размера w × w):

function mul(a, b : tmatr) : tmatr;
var res : tmatr;
    i, j, t : integer;
begin
    for i := 1 to w do begin
        for j := 1 to w do begin
            res[i][j] := 0;
            for t := 1 to w do begin
                res[i][j] := res[i][j] + a[i][t]*b[t][j];
            end;
        end;
    end;
    mul := res;
end;

function power(a : tmatr; b : integer) : tmatr;
var i, j : integer;
    res, tmp : tmatr;
begin
    res := E; // единичная матрица
    tmp := a;
    while (b > 0) do begin
        if (b mod 2 = 1) then res := mul(res, tmp);
        b := b div 2;
        tmp := mul(tmp, tmp);
    end;
    power := res;
end;

Как уже говорилось, будет сделано O(log b) перемножений. В данном случае, на каждое перемножение тратится n³ операций (где n -- размерность матрицы). Так что этот алгоритм будет работать за O(n³log b).

Вернемся к (3). Матрицу D мы умеем вычислять за O((2ⁿ)²n) = O(4ⁿn) (как в рассмотренных задачах). Вектор a[m] сумеем найти за O((2ⁿ)³log b) = O(8ⁿlog m). В итоге получаем асимптотику O(8ⁿlog m). При больших m (например, 10¹⁰⁰) этот способ вычисления A несравнимо лучше наивного.