Теоретический материал (С++): Функции

Теоретический материал (С++)

Функции (часть 1)

В предыдущем листке была задача вычисления числа сочетаний из n элементов по k, для чего необходимо вычисление факториалов трех величин: n, k и n-k. Для этого можно сделать три цикла, что приводит к увеличению размера программы за счет трехкратного повторения похожего кода. Вместо этого лучше сделать одну функцию, вычисляющую факториал любого данного числа n и трижды использовать эту функцию в своей программе. Соответствующая функция может выглядеть так:

     int factorial (int n)
     {
         int f=1,i;
         for(i=2;i<=n;++i)
         {
             f=f*i;
         }
         return f;
     }

Этот текст должен идти до основной программы, то есть до функции main(). Первая строчка этого примера является описанием нашей функции. factorial – идентификатор, то есть имя нашей функции. После идентификатора в круглых скобках идет список параметров, которые получает наша функция. Список состоит из перечисленных через запятую типов параметров и их идентификаторов. В нашем случае список состоит из одной величины n, имеющей тип int: наша функция вычисляет факториал целого числа. Функция вычисляет целочисленную величину, поэтому функция будет возвращать значение типа int, что указывается до идентификатора функции. Функция может не возвращать никакого значения, тогда в качестве типа возвращаемого значения должно быть указано слово void.

Далее идет тело функции в фигурных скобках. Внутри функции вычисляется значение факториала числа n и оно сохраняется в переменной f. Функция завершается инструкцией return f, которая завершает работу функции и возвращает значение переменной f. Инструкция return может встречаться в произвольном месте функции, ее исполнение завершает работу функции и возвращает указанное значение в место вызова. Если функция не возвращает значения, то инструкция return используется без возвращаемого значения, также в функциях, не возвращающих значения, инструкция return может отсутствовать.

Функция должна быть описана до начала основной программы. Сама же основная программа, как можно догадаться, также является функцией с именем main, не получающая никаких параметров и возвращающее значение типа int.

Теперь мы можем использовать нашу функцию factorial в основной программе нахождения числа сочетаний:

     int main ()
     {
         int n,k;
         cin>>n>>k;
         cout<<factorial(n)/(factorial(k)*factorial(n-k))<<endl;
         return 0;
     }

В этом примере мы трижды вызываем функцию factorial для вычисления трех факториалов: factorial(n), factorial(k), factorial(n-k).

Мы также можем объявить функцию binomial, которая принимает два целочисленных параметра n и k и вычисляет число сочетаний из n по k:

     int binomial (int n, int k)
     {
         return factorial(n)/(factorial(k)*factorial(n-k));
     }

Тогда в нашей основной программе мы можем вызвать функцию binomial для нахождения числа сочетаний:

cout<<binomial(n,k)<<endl;

Поскольку в этом случае функция main вызывает функцию binomial, а функция binomial вызывает функцию factorial, а каждая функция должна быть описана до ее вызова из другой функции, то порядок описания функций в программе должен быть такой:

int factorial (int n)

int binomial (int n, int k)

int main ()

Вернемся к задаче нахождения наибольшего из двух или трех чисел. Напишем функцию, находящую максимум из двух данных чисел:

     double max (double a, double b)
     {
         if (a>b)
             return a;
         else
             return b;
     }

Теперь мы можем реализовать функцию max, находящую максимум трех чисел:

     double max (double a, double b, double c)
     {
         return max( max(a,b), c);
     }

В данном примере написаны две различные функции max: первая с двумя параметрами, вторая с тремя параметрами. Несмотря на то, что функции имеют одинаковые имена, по количеству передаваемых параметров ясно, какая из них имеется в виду. В нашем случае функция max (double a, double b, double c) дважды вызывает функцию max для двух чисел: сначала, чтобы найти максимум из a и b, потом чтобы найти максимум из этой величины и c.

Упражнения

(A) Напишите функцию int min (int a, int b, int c, int d), находящее наименьшее из четырех данных чисел. Функция main дожна считывать четыре числа с клавиатуры, вызывать функцию min, выводить результат ее работы на экран.
(B) Напишите функцию double power (double a, int n), вычисляющую значение aⁿ . Функция main должна считывать числа a и n, вызывать функцию power, выводить результат ее работы на экран.
(C) Напишите функцию bool Xor (bool x, bool y), реализующую функцию "Исключающее ИЛИ" двух логических переменных x и y. Функция Xor должна возвращать true, если ровно один из ее аргументов x или y, но не оба одновременно равны true. Функция main в программе должна запрашивать значения переменных x и y, (два числа, равных 0 или 1), вызывать функцию Xor(x,y) и выводить результат на экран.
(D) Напишите "функцию голосования" bool Election(bool x, bool y, bool z), которая возвращает то значение (true или false), которое среди значений ее аргументов x, y, z встречается чаще. Функция main должна запрашивать три числа, равных 0 или 1, вызывать функцию Election и выводить результат на экран.
(E) Напишите функцию bool IsPrime (int n), возвращающую true, если натуральное число n>1 простое, и false, если составное.
Функция main должна запрашивать число с клавиатуры, вызывать функцию IsPime, выводить строку prime, если число простое или composite, если число составное.
Указание: число является составным, если оно имеет натуральный делитель, отличный от 1 до n. Программа должна проверить делимость числа n на все числа от 2 до n-1 и вернуть false при нахождении нетривиального делителя. Для того, чтобы проверить, что число n делится на число d нацело, необходимо сравнить остаток от деления n на d с нулем.

Рекурсия

                      Эпиграф:
                        void ShortStory()
                        {
                            cout<<"У попа была собака, он ее любил."<<endl;
                            cout<<"Она съела кусок мяса, он ее убил,"<<endl;
                            cout<<"В землю закопал и надпись написал:"<<endl;
                            ShortStory();
                        }

Как мы видели выше, функция может вызывать другую функцию. Но функция также может вызывать и саму себя! Рассмотрим это на примере функции вычисления факториала. Хорошо известно, что 0!=1, 1!=1. А как вычислить величину n! для большого n? Если бы мы могли вычислить величину (n-1)!, то тогда мы легко вычислим n!, поскольку n!=n(n-1)!. Но как вычислить (n-1)! ? Если бы мы вычислили (n-2)!, то мы сможем вычисли и (n-1)!=(n-1)(n-2)!. А как вычислить (n-2)! ? Если бы... В конце концов, мы дойдем до величины 0!, которая равна 1. Таким образом, для вычисления факториала мы можем использовать значение факториала для меньшего числа. Это можно сделать и в программе на C++:

     int factorial (int n)
     {
         if (n==0)
             return 1;
         else
             return n*factorial(n-1);
     }

Подобный прием (вызов функцией самой себя) называется рекурсией, а сама функция называется рекурсивной.

Рекурсивные функции являются мощным механизмом в программировании. К сожалению, они не всегда эффективны (об этом речь пойдет позже). Также часто использование рекурсии приводит к ошибкам, наиболее распространенная из таких ошибок – бесконечная рекурсия, когда цепочка вызовов функций никогда не завершается и продолжается, пока не кончится свободная память в компьютере. Пример бесконечной рекурсии приведен в эпиграфе к этому разделу. Две наиболее распространенные причины для бесконечной рекурсии:

Неправильное оформление выхода из рекурсии. Например, если мы в программе вычисления факториала забудем поставить проверку if (n==0), то factorial(0) вызовет factorial(-1), тот вызовет factorial(-2) и т.д.
Рекурсивный вызов с неправильными параметрами. Например, если функция factorial(n) будет вызывать factorial(n), то также получиться бесконечная цепочка.

Поэтому при разработке рекурсивной функции необходимо прежде всего оформлять условия завершения рекурсии и думать, почему рекурсия когда-либо завершит работу.

Упражнения

(B) Напишите рекурсивную функцию возведения в степень, пользующуюся следующим свойством: aⁿ=a*a^n-1.
(F) Напишите функцию возведения в степень, которая работала бы как для положительных, так и для отрицательных значений n: a^-n=1/aⁿ.
(G) Напишите функцию быстрого возведения в степень, которая пользовалась бы следующими свойствами: aⁿ=(a^n/2)² при четном n, aⁿ=a*a^n-1 при нечетном n. Подумайте, сколько умножений выполнит эта функция для вычисления aⁿ?
(H) Последовательность Фибоначчи определена следующим образом: φ₀=1, φ₁=1, φ_n=φ_n-1+φ_n-2
при n>1. Начало ряда Фибоначчи выглядит следующим образом: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... Напишите функцию int phi(int n), которая по данному натуральному n возвращает φ_n. Функция n должна считывать значение n и выводить значение n-го числа Фибоначчи.
(I) Для биномиальных коэффициентов (числа сочетаний из n по k) хорошо известна рекуррентная формула: C_n^k=C_n-1^k-1+C_n-1^k. Вычислите значение C_n^k, пользуясь этой формулой и учитывая, что C_n⁰=C_nⁿ=1.
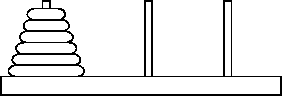
(J) Головоломка "Ханойские башни" состоит из трех колышков, пронумерованных числами 1, 2, 3. На колышек 1 надета пирамидка из n дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного колышка на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку с колышка 1 на колышек 2 за минимальное число перекладываний.
Напишите программу, которая решает головоломку – для данного числа дисков n печатает последовательность перекладываний в формате "Disk 1 move from 1 to 2" (диск 1 переложить c колышка 1 на колышек 2), печатая по одной инструкции в строке. Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
Программа должна вывести минимальный (по количеству произведенных операций) способ перекладывания пирамидки.

Указание: подумайте, как переложить пирамидку из одного диска? Из двух дисков? Из трех дисков? Из четырех дисков? Напишите функцию void move (int n, int x, int y), которая перекладывает пирамидку высоты n с колышка номер x на колышек номер y.