Игры и стратегии

Мы начнем с простой игры, которая называется "Квадраты".

Правила игры:

Игра начинается с произвольного целого неотрицательного числа (например, 75). Два игрока по очереди вычитают из него натуральные числа, являющиеся полными квадратами (то есть 1, 4, 9, 16, 25 и т.д.), так чтобы оставшееся число было неотрицательным. Проигрывает тот, кто не может сделать очередной ход. Вот как, например, может протекать игра:

На этом рисунке ходы первого игрока изображены красной стрелкой, а ходы второго — зеленой.

Мы видим, что в приведенном примере второй игрок выиграл, поскольку у первого нет больше допустимых ходов. Но возникает сомнение: играл ли первый игрок достаточно хорошо? Мог ли он выиграть, действуя по-другому? Если бы оба игрока играли наилучшим образом, с каким результатом закончилась бы эта партия?

Предположим, что игра начинается с неотрицательного числа n. Возможны два исхода:

• первый игрок имеет стратегию, позволяющую ему выиграть при любых действиях второго;
• такой стратегии у первого игрока нет, поэтому второй всегда может выиграть.

В первом случае будем называть число n выигрышным, а во втором — проигрышным.

Разберем простые примеры.

• 0 — безусловно проигрышное число, потому что в этой позиции нельзя сделать ни одного хода.
• Любой полный квадрат — 1, 4, 9, 16, ... — выигрышное число, потому что можно за один ход превратить его в ноль, предложив противнику проигрышную позицию.

Путем несложных рассуждений можно заполнить такую таблицу:

Таблица 1.

Здесь и далее будем обозначать выигрышную клетку - счастливым смайликом, а проигрышную - грустным.

Можно сформулировать правило, по которому заполняется такая таблица:

Рассмотрим пример работы этого правила. Для этого продолжили таблицу 1 и заполним ее для всех n вплоть до 21. Получится:

Теперь можно проанализировать число 22: будет ли оно выигрышным или проигрышным. Из этого числа возможно сделать такие ходы:

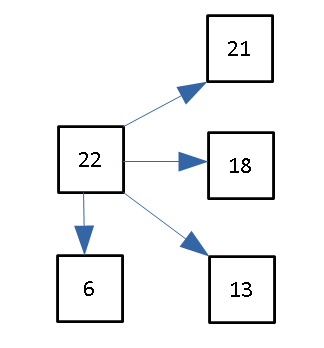
Каждое из четырех полученных чисел — 6, 13, 18, 21 — выигрышное. Поэтому само число 22  — проигрышное. Таким способом мы можем легко исследовать любую начальную позицию в этой игре.

Мало просто знать, что позиция, в которой вы оказались — выигрышная. Надо еще суметь сделать правильный ход.

Пример 1.

Начальная позиция: n=19. Какой первый ход нужно сделать?

Решение:

Взгляните на таблицу 2.

Число 19 — выигрышное. Для победы нам необходимо выбрать такой ход, после которого сопернику достанется проигрышная позиция.

У нас всего 4 варианта: 18 (19-1), 15 (19-4), 10 (19-9) и 3 (19-16).

Вновь обратимся к таблице 2, и выберем из наших четырех чисел проигрышные. Нам подходят числа 15 и 10: любой из этих ходов оставит сопернику проигрышное число.

Пример 2.

Из начального числа n=18 первый игрок вычел 4, оставив сопернику число 14. Что делать дальше?

Решение:

И вновь воспользуемся таблицей 2.

Мы видим, что 14 — выигрышное число (первый игрок сделал не самый лучший ход!). Поэтому у второго игрока появилась возможность выиграть партию. Для этого ему нужно оставить первому игроку проигрышное число, например, 10. Победа!

---

Сейчас мы приведем более эффективный способ определения выигрышных и проигрышных позиций. Этот метод похож на решето Эратосфена, позволяющее находить все простые числа в заданном диапазоне. Предположим, что нам хочется определить исходы всех игр с начальными значениями от 0 до 15.

Мы знаем, что 0 — проигрышное число, и отметим это в таблице:

Добавляя к числу 0 квадраты, мы получаем числа 1, 4, 9, которые являются выигрышными, потому что из них можно попасть в проигрышное число 0:

Самое маленькое непомеченное число — 2 — проигрышное, потому что иначе мы бы его уже пометили:

Прибавляя к числу 2 квадраты, получаем новые выигрышные числа (2+1, 2+4, 2+9) :

Следующее непомеченное число — 5 — снова проигрышное. Продолжая так и далее, мы заполним всю таблицу:

---

Пример 3.

Представьте, что вам досталось начинать игру с проигрышного числа 17. Надежды нет?

Решение:

Только без паники. Теоретически, ваш противник имеет выигрышную стратегию. Но кто вам сказал, что он достаточно хорошо знает математику, и не сделает ошибки по ходу игры?

Но представьте на минуту, что первым ходом вы вычитаете из 17 число 16 и оставляете сопернику 1. Тут уже ему ничего не остается, кроме как сделать последний победный ход. Значит, стоит оставлять число как можно большее? И это не так. Самое большое число, которое вы сможете оставить — 16. Но оно является полным квадратом, и второй игрок тут же оставит вам ноль. На самом деле, нужно оставлять такое число, чтобы для победы второму игроку оставалось как можно больше ходов.

Будем называть удаленностью позиции n число, определяемое по следующим правилам:

Удаленность позиции характеризует количество ходов, необходимых для завершения партии.

Приведенное выше правило основывается на простой идее. Игрок, имеющий выигрышную стратегию, стремится победить как можно быстрее, чтобы свести к минимуму возможность случайной ошибки при выборе очередного хода. Поэтому среди всех возможных ходов он будет выбирать такой, чтобы удаленность нового числа была как можно меньше. Прибавляемая единица соответствует ходу, который игрок делает сейчас.

Проигрывающий же старается как можно дольше оттягивать свое поражение, надеясь на оплошность соперника. Поэтому из всех возможных ходов он должен выбрать число с максимальной удаленностью.

Продемонстрируем, как работает это правило. Пусть мы уже вычислили удаленности всех позиций до n=16, и теперь хотим узнать, чему же равна удаленность числа 17.

Из числа 17 можно получить числа 16, 13, 8 или 1.

Их удаленности равны 1, 7, 5, 1 соответственно.

Поскольку число 17 — проигрышное, его удаленность на 1 больше, чем наибольшая из удаленностей чисел 16, 13, 8, 1, то есть равна 7+1=8. Из проигрышного числа нужно всегда делать ход в то число, удаленность которого наибольшая возможная. В данном случае это число 13.

В завершение заметим, что нечетное значение удаленности соответствует выигрышным позициям, а четное — проигрышным.

---

Ним Витхоффа. Правила игры.

Дана пара неотрицательных целых чисел (которые могут быть равны). Два игрока ходят по очереди. За один ход разрешается:

• либо вычесть любое число из одного из данных;
• либо вычесть из обоих данных чисел одно и то же число.

При этом требуется, чтобы оба числа оставались неотрицательными.

Проигрывает тот, кто не может сделать хода (то есть игрок, который оставляет своим ходом получает позицию (0,0), выигрывает).

Эта игра эквивалентна игре "Ферзь Витхоффа", в которую играют на шахматной доске, на которой стоит изначально в клетке (n,m) стоит ферзь. За один ход разрешается передвинуть ферзя на любое количество клеток влево, вверх или влево-вверх. Выигрывает тот, кто приведет ферзя в клетку (0,0).

Мы можем проанализировать эту игру так же, как предыдущую.

Во-первых, также верно будет соображение, что клетка с координатами (0; 0) является проигрышной. Отметим ее в таблице.

Во-вторых, любые клетки, из которых за 1 ход можно перейти в (0; 0) - являются выигрышными. Это клетки, расположенные на той же горизонтали, вертикали или диагонали:

Во-третьих, можно заметить 2 клети - с координатами (1; 2) и (2; 1) из которых можно попасть только в выигрышные клетки. Таким образом, эти клетки являются проигрышными.

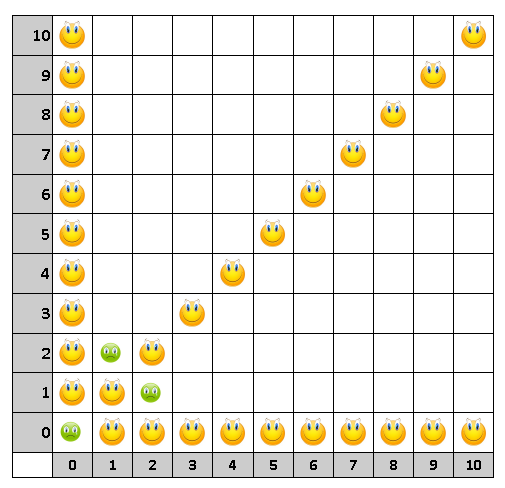
Клетки, из которых можно за 1 ход перейти в проигрышные (и таким образом "подарить" их сопернику) - являются выигрышными:

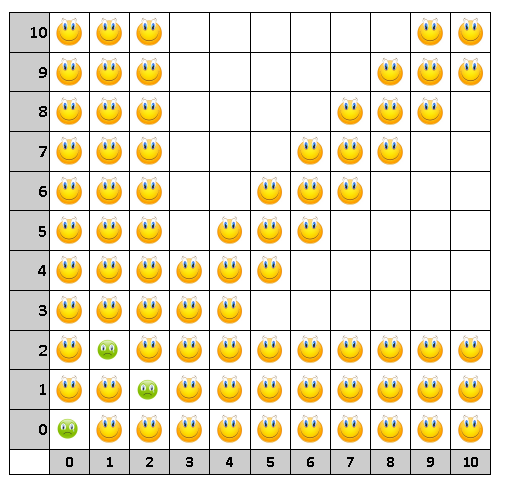
Продолжая так и далее, мы найдем проигрышные позиции (m, n) (m < n) : (0,0), (1,2), (3,5), (4,7), (6,10), (8,13), ... . Можно заметить и обобщить эту закономерность: чтобы найти (i+1)-ю проигрышную позицию, требуется найти наименьшее натуральное число k, которое не участвует в записи предыдущих позиций (ни на первом, ни на втором месте в паре). Искомая позиция —  (k, k+i).