Фишка на графе
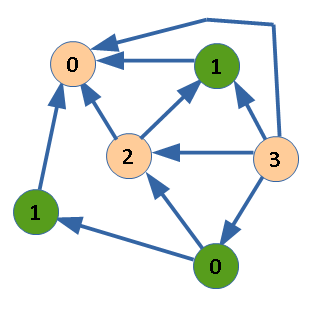
Правила игры. Дан ориентированный ациклический граф. В некоторой его вершине находится фишка. Играют двое, ходы делаются по очереди. За один ход можно переместить фишку в любую вершину, в которую существует ребро из текущей. Проигрывает тот, кто не может сделать следующий ход.
На рисунке показан пример графа. Положение фишки указано зеленым цветом.
Как и ранее, при анализе данной игры можно отметить выигрышные и проигрышные вершины.
При этом можно использовать такие соображения:
- начать можно с того, что вершины, из которых не выходит ни одного ребра, будут проигрышными (то есть, если перед ходом какого-то игрока фишка стоит в такой вершине, то он проиграл, так как не сможет сделать ход)
- любая вершина, из которой есть хотя бы одно ребро, ведущее в проигрышную — будет выигрышной;
- любая вершина, из которой можно попасть только в выигрышные — сама является проигрышной.
Так как в перспективе мы собираемся рассмотреть сумму из таких игр, то в данной задаче будем не просто выяснять является ли вершина выигрышной или проигрышной, а для каждой вершины будем вычислять функцию Шпрага-Гранди.
Эта функция определяется таким образом:
- для всех вершин, не имеющих исходящих ребер, функция F(v) = 0;
- для всех остальных вершин функция будет вычисляться так: рассмотрим все ребра, исходящие из данной вершины. Пусть эти ребра ведут в вершины v1, v2…, vk. Тогда F(v) — находится как наименьшее целое неотрицательное число, которого нет среди F(v1), F(v2), .. F(vk).
На примере ранее изображенного графа покажем процесс вычисления.
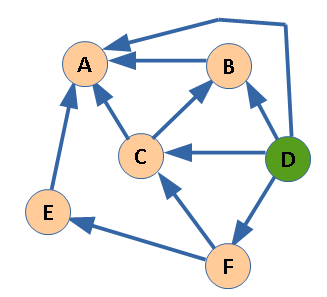
Единственной вершине без исходящих ребер (A) припишем значение 0.
Теперь у нас есть все данные, чтобы вычислить F(B). Из вершины B есть ребро только в A, и F(A)=0. Минимальное "незанятое" число, таким образом, будет 1.
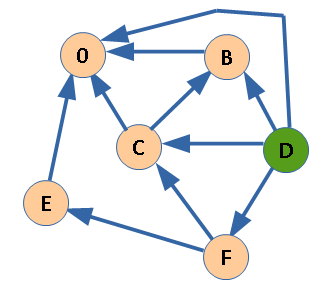
Можно вычислить F(С). Из вершины С есть ребра в A и B, и F(A)=0 и F(B)=1. Минимальное "незанятое" число будет 2.
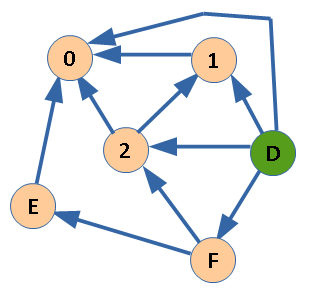
F(E) вычисляется аналогично F(B).
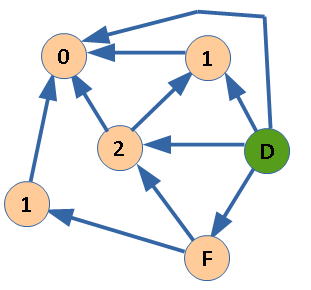
Из вершины F есть ребра в С и E. F(C)=2, F(E)=1. Не занято число 0. Обратите внимание, что без значения F(F) нельзя вычислить F(D), так как для вычисления функции для вершины надо знать ее значение для всех вершин, куда есть исходящие ребра.
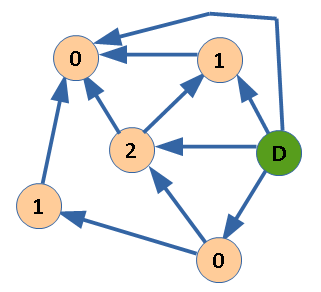
И, наконец, F(D). Из вершины D есть ребра в B, C и F. F(B)=1, F(C)=2, и F(F)=0. Наименьшее неотрицательное число = 3.
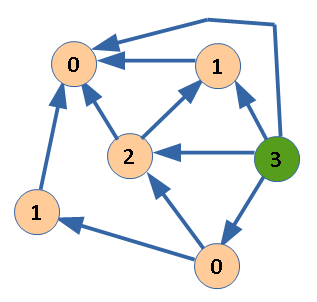
Функция Шпрага-Гранди равна нулю для всех проигрышных вершин и положительна для всех выигрышных.
Для того, чтобы ответить на вопрос «кто выиграет?» достаточно вычислить функцию для той вершины, где в начальный момент находится фишка.
Чтобы ответить на вопрос: «какой ход нужно сделать из определенной позиции?» нужно рассмотреть все исходящие ребра для текущей вершины. Если вершина является выигрышной, то, по построению, из нее обязательно будет хотя бы один ход в одну из проигрышных. Этот ход и нужно делать.
Усложним задачу: много фишек на графе
Правила игры. Дан ориентированный ациклический граф. В некоторых его вершинах находятся фишки. Играют двое, ходы делаются по очереди. За один ход можно переместить фишку в любую вершину, в которую существует ребро из текущей. Проигрывает тот, кто не может сделать следующий ход. В процессе игры разрешается размещать несколько фишек в одной вершине.
Эта игра является суммой нескольких предыдущих игр.
То есть, ее можно рассматривать как несколько одновременно происходящих игр, каждая из которых ведется с единственной фишкой. В этом случае перед игроком появляется дополнительная задача.
Во-первых, следует правильно выбрать в какой из элементарных игр он будет делать ход (какую фишку он будет двигать). При этом данная элементарная игра не должна быть завершена (ход этой фишкой должен быть возможен).
Во-вторых, следует сделать правильный ход выбранной фишкой.
Для этого мы будем использовать функцию Шпрага-Гранди.
- Вычислим F(v) для всех вершин графа;
- Рассмотрим все вершины, в которых находятся фишки. Тогда общим значением функции F для суммарной позиции будет F = F(v1) XOR F(v2) XOR … XOR F(vk) (где v1...vk) – вершины, в которых стоят фишки).
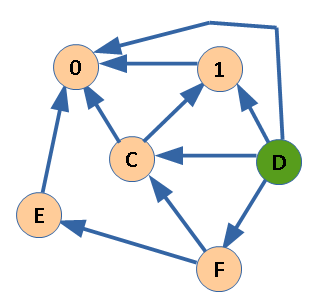
В качестве примера будем использовать граф из предыдущей задачи, для которого уже вычислены значения функции Шпрага-Гранди. Только установим дополнительные фишки, их расположение показано зеленым цветом.
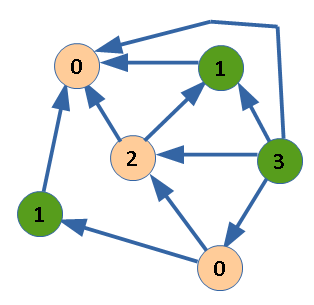
Для оценки позиции по сумме игр нужно найти:
F(B)XOR F(D) XOR F(E) = 1 XOR 3 XOR 1 = 3.
Если вычисленное значение F = 0, то позиция по сумме игр — проигрышная (что не означает проигрыша во всех играх суммы. В отдельных играх суммы возможен выигрыш).
Если вычисленное значение F > 0, то позиция по сумме игр — выигрышная (что, опять же, не означает выигрыша во всех играх суммы. В отдельных играх возможен проигрыш).
Правильным будет ход, который приведет к позиции с F = 0 (то есть после которого сопернику достанется проигрышная позиция).
В приведенном примере необходимо сделать ход фишкой из вершины D в вершину F. Таким образом F(B) xor F(E) xor F(F) = 0.