Методы глобальной оптимизации

Идея реализации

Как уже было написано в предыдущей статье, целью работы данного метода является нахождения минимума некоторой целевой функции F(x₁, x₂, x₃, ..., x_k).

Более того, хотелось бы не ошибиться при поиске и не принять просто оптимальный вариант (локальный минимум) за самый оптимальный (глобальный минимум).

На рисунке буквами обозначены точки разных минимумов некоторой функции. В это случае, разумеется, хотелось бы после работы алгоритма получить точку A, не точки B, C или D.

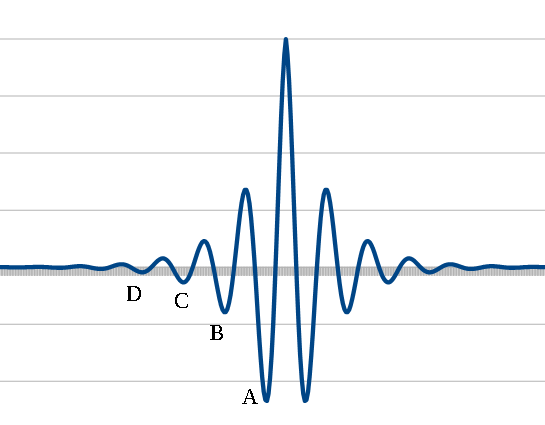
Чтобы избежать "застревания" в локальных минимумах, процесс поиска иногда делают на основе случайных чисел. Это увеличивает шансы обнаружить глобальный минимум.

Алгоритм основывается на имитации физического процесса, который происходит при кристаллизации вещества. Предполагается, что атомы уже выстроились в кристаллическую решётку (которая является энергетически выгодной структурой), но ещё допустимы переходы отдельных атомов из одной ячейки в другую.

Процесс кристаллизации протекает при постепенно понижающейся температуре. Переход атома из одной ячейки в другую происходит с некоторой вероятностью, причём вероятность уменьшается с понижением температуры. (Поскольку температура является характеристикой для энергии атомов вещества, то чем больше у атома энергии, тем больше шансов поменять свое местоположение в кристаллической решетке)

В какой-то момент температура опускается до предельного значения, при котором ни одному атому не хватит энергии, чтобы покинуть свое место в кристаллической решетке. Это соответствует окончанию процесса кристаллизации.

Процесс имитации отжига можно представить в виде такой схемы:

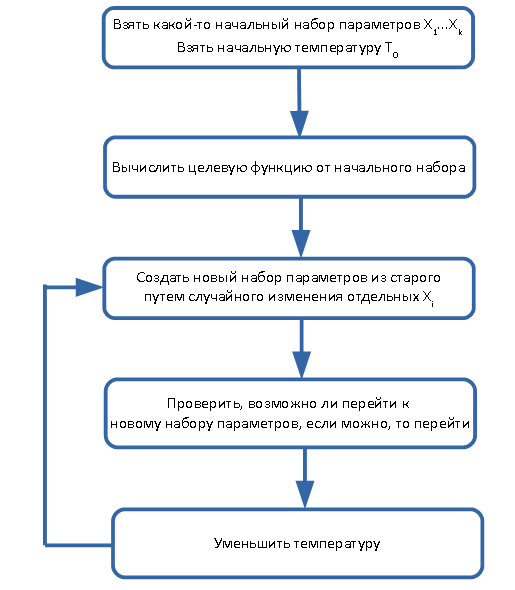
Температура - это некоторая числовая величина, от которой будет зависеть возможность перехода между двумя вариантами (старым и новым). Также температура будет использоваться для проверки окончания цикла - он заканчивается, когда температура стала достаточно маленькой.

На рисунке представлена формула вероятности перехода от набора X_i к набору X_i+1

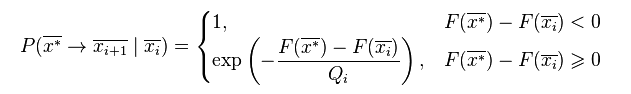
Данная формула означает:

• Если новый набор параметров оптимальнее (значение целевой функции F() для него меньше), то переход делается обязательно (вероятность = 1);
• Если значение целевой функции F() для нового набора больше, то переход делается с некоторой вероятностью, зависящей от текущей температуры (Q_i) и того, насколько отличается значение целевой функции на новом и старом наборе (чем больше температура и чем менее глубокий минимум мы сейчас рассматриваем, тем больше шансов из него "выпрыгнуть");

С точки зрения реализации, второй пункт означает, что необходимо взять случайное число в интервале от 0 до 1, и если это число будет ≤ выражению, вычисленному по формуле, то переход производится.

Закономерно могут возникнуть вопросы по реализации алгоритма. Например:

• какую начальную температуру брать?
• по какому закону уменьшать температуру?
• как на базе имеющегося варианта сгенерировать новый?

Ответ на эти вопросы содержится в "Теореме о бесплатных завтраках", которая гласит, что