Постановка задачи
Пусть дан массив, состоящий из N целых чисел (для определенности: пусть нумерация начинается с нуля).
К массиву ожидается достаточно большое количество запросов. Каждый запрос требует нахождении суммы элементов на интервале [left; right] (где left и right – номера самого левого и самого правого элемента, включительно).
Требуется создать такую структуру данных и метод работы с ней, чтобы скорость ответа на такой запрос была выше, чем у тривиального алгоритма.
Идея реализации
Разобьем массив на блоки, длины ceil(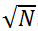 ), где ceil() – операция округления до ближайшего сверху целого. Таких блоков будет ровно
), где ceil() – операция округления до ближайшего сверху целого. Таких блоков будет ровно 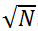 .
.
Для каждого блока вычислим сумму элементов в нем, и запишем в массив block_sum[].
Теперь ответ на запрос о сумме элементов на интервале можно получить за время O(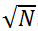 ).
).
Если какой-то блок целиком принадлежит интервалу, можно использовать уже готовую сумму этого блока.
Если на интервале лежит только часть блока, к этой части можно применить тривиальный алгоритм подсчета суммы.
При этом, неполных блоков будет не более двух (первый и последний).
В худшем случае, для расчета суммы по каждому из неполных блоков требуется 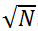 - 1 операция.
- 1 операция.
Также, в худшем случае, потребуется суммирование 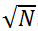 - 2 блоков.
- 2 блоков.
Пример работы алгоритма
Пусть дан массив из 9 элементов. Тогда длина блока будет равна 3, количество блоков также будет 3.
В случае, если потребуется вычислить сумму элементов на интервале [1; 7] (как показано на рисунке).

- Будут сделаны следующие вычисления:
- Первый блок входит в запрашиваемый интервал не полностью, поэтому для него будет использован тривиальный алгоритм: 2 + 1 = 3 (сумма элементов из первого блока);
- Второй блок находится на интервале, поэтому сумма его элементов уже известна и равна 14;
- Третий блок входит в интервал частично, поэтому сумму в нем будем также считать поэлементно: 7 + 4 = 11.
Итого: 3 + 14 + 11 = 28.
Реализация