Поиск минимального/максимального элемента на интервале
Реализация аналогична поиску суммы элементов на интервале, за исключением того, что теперь вычисляться будет массив block_min[] (block[max]). Время работы данного алгоритма также останется пропорциональным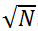 
Изменения всех элементов интервала с запросом о величине отдельных элементов
Пусть дан массив, для которого возможны два вида запросов:
- увеличить/уменьшить все элементы интервала [left; right] на одну и ту же величину;
- получить значение i-го элемента массива;
Идея реализации:
В этом случае для каждого блока будем хранить величину изменений, которые касаются элементов всего блока. Если изменения касаются только части блока, то такие элементы будут изменяться по отдельности.
Например, в случае данных, указанных на рисунке значение элемента a[3] будет равно 5 + 6 = 11, а значение элемента a[1] будет равно 2+(-5) = -3.
Применим к массиву, указанному на рисунке операцию «Прибавить 10 ко всем элементам интервала [0; 4]»
В этом случае произойдут следующие изменения:
- первый блок полностью принадлежит изменяемому интервалу, поэтому его изменения будут фиксироваться в массиве block_additive[].
- второй блок лежит в изменяемом интервале частично, поэтому все изменения будут производиться непосредственно с элементами.
Результат изменений показан на рисунке, измененные значения выделены серым фоном:
Изменение всех элементов на интервале с запросами о сумме элементов интервала
Идея реализации аналогична предыдущей задаче, за исключением того, что теперь требуется хранить два массива для описания блоков: массив для фиксации изменений и массив для хранения сумм элементов блока.
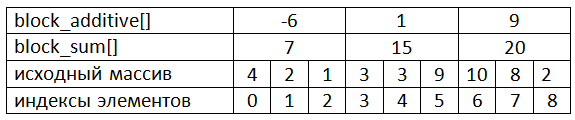
Возможное состояние для исходного массива из 9 элементов показано на рисунке.
Задача о поддержании множества
Пусть есть множество чисел, для которого возможны операции добавления/удаления элемента, запрос k-го по порядку элемента и запрос о принадлежности числа X множеству.
Идея реализации. Будем хранить числа в упорядоченном виде блоками по 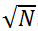штук. Для каждого блока будем хранить наименьшее и наибольшее число (в этом случае легко выполняется проверка на возможную принадлежность числа X конкретному блоку).
При добавлении/удалении элементов требуется выполнять переформирование блоков, поэтому для хранения блока следует использовать структуру данных, позволяющую за время O(1) выполнять удаление/добавление как первого, так и последнего элемента.
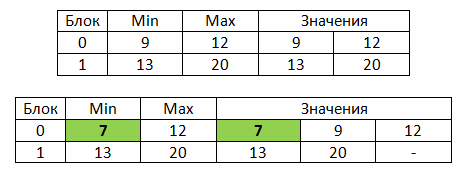
Пример переформирования блоков показан на рисунке.
Пусть в начале было множество из четырех элементов (9, 12, 13, 20), добавление нового элемента (7) ведет к изменению длины блока и расположения элементов в блоках. Добавляемое число выделено зеленым цветом.
