Постановка задачи
Пусть дана некоторая структура данных, к которой возможны запросы двух видов: чисто информационные (о состоянии структуры или отдельных элементов) и модифицирующие (требующие изменения отдельного элемента или группы элементов).
Как и ранее, хотелось бы получить такой алгоритм работы, время выполнения которого было бы заметно меньше, нежели время работы тривиального алгоритма.
Под тривиальным алгоритмом будем подразумевать выполнение по очереди всех запросов в порядке поступления.
Оценим время работы тривиального алгоритма.
Пусть k запросов являются информационными, и m – модифицирующими. Пусть Z - общее число запросов (Z = k + m)
На любой информационный запрос можно дать ответ за время O(1).
В худшем случае, каждый модифицирующий запрос будет выполняться за O(N) операций.
Таким образом, итоговое время работы можно оценить как O(k + mN).
В самом худшем случае, практически все запросы будут модифицирующими, то есть итоговая сложность будет O(N*Z).
Идея реализации
Рассмотрим пример
Пусть дан числовой массив a[], и возможны запросы вида:
- узнать, чему равно текущее значение a[i];
- изменить элементы массива на интервале [left; right] на некоторую величину delta.
Разобьем входные запросы на блоки длины 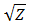 , где Z - общее количество запросов.
, где Z - общее количество запросов.
Будем обрабатывать запросы поблочно
- если запрос является модифицирующим, то пропустим его;
- если запрос является информационным, то возьмем элемент a[i] и просмотрим все модифицирующие запросы, которые могли менять его значение. Вычислим значение элемента a[i] с учетом этих запросов и вернем в качестве результата (сам элемент a[i] при этом не меняется;
- если достигнут конец блока, то применим к массиву a[] все модифицирующие запросы данного блока (содержимое массива изменяется только на этом этапе). После обновления данных, начнем снова обрабатывать запросы по такому же алгоритму.
Последний пункт (обновление при достижении границы блока) можно выполнить за время O(N + 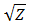 )
)
Оценим время работы такого алгоритма обработки запросов.
Обработка каждого блока запросов занимает не более O(Z) операций.
Модификация данных на границе каждого блока занимает не более O(N + 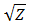 ).
).
При этом общее количество блоков равно 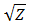
Из оценки видно, что данный метод требует в общем случае аккуратного подхода в зависимости от количества запросов, простоты ответа на информационный запрос и скорости проведения модификации над исходными данными.