Рассмотрим пример.
Пусть дан массив, содержащий N целых чисел. Пусть также ожидается Z запросов вида [left; right] - количество различных чисел на указанном интервале.
Оценим для начала реализацию тривиальным алгоритмом. В худшем случае потребуется время O(Z*N2). Под худшим случаем подразумевается, что все запросы будут по длине интервала близки к размеру массива.
Обратим внимание, что при тривиальной реализации каждый запрос обрабатывается отдельно и результаты одного запроса никак не учитываются в последующих.
Рассмотрим интервал [a; b]. Пусть нам известен ответ на запрос для этого интервала и он равен X. Тогда для вычисление ответа для запроса [a; b + 1] можно выполнить за линейную сложность (что проще квадратичной, которая используется в тривиальной реализации). Аналогично, сравнительно быстро можно получить ответ для запроса [a - 1; b].
Воспользуемся этими соображениями. Разобьем запросы на группы по значению левой границы интервала. Пусть количество групп будет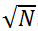 
. Упорядочим запросы в каждом блоке также по возрастанию правой границы интервала.
Будем обрабатывать запросы поблочно. Ответ на первый запрос посчитаем с помощью тривиального алгоритма. Ответы на следующие запросы вычисляются, опираясь на ранее полученные результаты.
Время работы для одного блока запросов можно оценить как: O(zN + z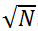). Где z - количество запросов в блоке. Левая граница запросов может двигаться только в пределах группы, поэтому для перерасчета ответа из-за ее сдвига потребуется не более O(z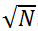). Правая граница при этом может перемещаться в границах всего массива, и перерасчеты из-за ее сдвига будут занимать O(zN).
В целом по алгоритму оценка времени будет выглядеть как: O(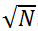(ZN + Z)).
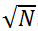Таким образом, удалось улучшить оценку для тривиального алгоритма.
Сформулируем требования к задачам, для которых можно применять аналогичную эвристику.
- Запросы к данным должны быть только информационные (без модифицирующих).
- Должна существовать сравнительно простая возможность пересчета ответа на запрос при изменении правой или левой границы на единицу.