Двумерные массивы (вложенные списки)

Часто в задачах приходится хранить прямоугольные таблицы с данными. Такие таблицы называются матрицами или двумерными массивами. В языке программирования Python таблицу можно представить в виде списка строк, каждый элемент которого является в свою очередь списком, например, чисел. Например, создать числовую таблицу из двух строк и трех столбцов можно так:

A = [ [1, 2, 3], [4, 5, 6] ]

Здесь первая строка списка A[0] является списком из чисел [1, 2, 3]. То есть

A[0][0] == 1
A[0][1] == 2
A[0][2] == 3

A[1][0] == 4
A[1][1] == 5 
A[1][2] == 6

Для обработки и вывода списка как правило используется два вложенных цикла. Первый цикл по номеру строки, второй цикл по элементам внутри строки. Например, вывести двумерный числовой список на экран построчно, разделяя числа пробелами внутри одной строки, можно так:

for i in range(len(A)):
    for j in range(len(A[i]):
        print(A[i][j], end=" ")
    print()

То же самое, но циклы не по индексу, а по значениям списка:

for row in A:
    for elem in row:
        print(elem, end=" ")
    print()

Кроме того, для вывода одной строки можно воспользоваться методом join:

for row in A:
    print(" ".join(list(map(str, row))))

Используем два вложенных цикла для подсчета суммы всех чисел в списке:

S = 0
for i in range(len(A)):
    for j in range(len(A[i])):
        S += A[i][j]

Или то же самое с циклом не по индексу, а по значениям строк:

S = 0
for row in A:
    for elem in row:
        S += elem

Создание вложенных списков

Пусть даны два числа: количество строк n и количество столбцов m. Необходимо создать список размером n*m, заполненный нулями.

Очевидное решение оказывается неверным:

A = [ [0] * m ] * n

В этом легко убедиться, если присвоить элементу A[0][0] значение 1, а потом вывести значение другого элемента A[1][0] — оно тоже будет равно 1! Дело в том, что [0] * m возвращает ccылку на список из m нулей. Но последующее повторение этого элемента создает список из n элементов, каждый из которых является ссылкой на один и тот же список, поэтому все строки результирующего списка на самом деле являются одной и той же строкой.

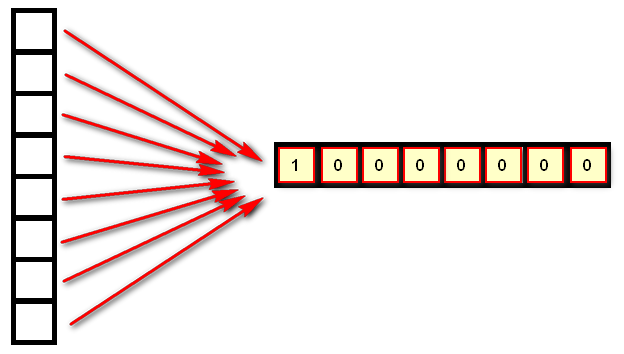
Выполнение операции B = A для списков также не создает новый список.

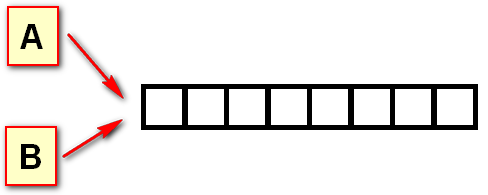
Таким образом, двумерный список нельзя создавать при помощи операции повторения одной строки таблицы. Что же делать?

Первый способ: сначала создадим список из n элементов (для начала просто из n нулей). Затем сделаем каждый элемент списка ссылкой на другой одномерный список из m элементов:

A = [0] * n
for i in range(n):
     A[i] = [0] * m

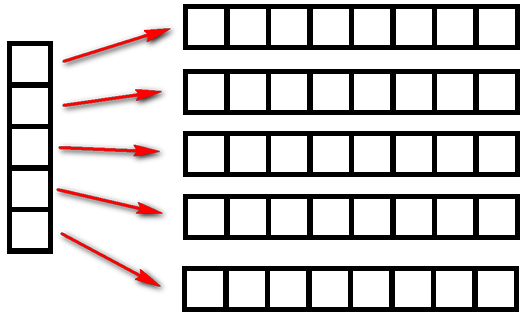
Другой (но похожий) способ: создать пустой список, потом n раз добавить в него новый элемент, являющийся списком-строкой:

A = []
for i in range(n):
    A.append([0] * m)

Но еще проще воспользоваться генератором: создать список из n элементов, каждый из которых будет списком, состоящим из m нулей:

A = [ [0]*m for i in range(n) ]

В этом случае каждый элемент создается независимо от остальных (заново конструируется список [0] * m для заполнения очередного элемента списка), а не копируются ссылки на один и тот же список. Подробнее о подобных генераторах будет рассказано ниже.

Ввод двумерного массива

Пусть программа получает на вход двумерный массив, в виде n строк, каждая из которых содержит m чисел, разделенных пробелами. Как их считать? Например, так:

A = []
for i in range(n):
    A.append(list(map(int, input().split())))

Или, без использования сложных вложенных вызовов функций:

A = []
for i in range(n):
    row = input().split()
    for i in range(len(row)):
        row[i] = int(row[i])
    A.append(row)

Можно сделать то же самое и при помощи генератора:

A = [ list(map(int, input().split())) for i in range(n) ]

Пример обработки двумерного массива

Пусть дан квадратный массив из n строк и n столбцов. Необходимо элементам, находящимся на главной диагонали, проходящей из левого верхнего угла в правый нижний (то есть тем элементам A[i][j], для которых i==j) присвоить значение 1, элементам, находящимся выше главной диагонали – значение 0, элементам, находящимся ниже главной диагонали – значение 2. То есть получить такой массив (пример для n==4):

1 0 0 0
2 1 0 0
2 2 1 0
2 2 2 1

Рассмотрим несколько способов решения этой задачи. Элементы, которые лежат выше главной диагонали – это элементы A[i][j], для которых i<j, а для элементов ниже главной диагонали i>j. Таким образом, мы можем сравнивать значения i и j и по ним определять значение A[i][j]. Получаем следующий алгоритм:

for i in range(n):
    for j in range(n):
    if i < j:
        A[i][j] = 0
    elif i > j:
        A[i][j] = 2
    else:
        A[i][j] = 1

Данный алгоритм плох, поскольку выполняет одну или две инструкции if для обработки каждого элемента. Если мы усложним алгоритм, то мы сможем обойтись вообще без условных инструкций.

Сначала заполним главную диагональ, для чего нам понадобится всего один цикл:

for i in range(n):
    A[i][i] = 1

Затем заполним значением 0 все элементы выше главной диагонали. Заметим, что для этой области в каждой строке с номером i номера столбцов меняются от i+1 до n-1 включительно. Для заполнения соответствующей части массива нам понадобятся вложенные циклы:

for i in range(n):
    for j in range(i + 1, n):
        A[i][j] = 0

Аналогично присваиваем значение 2 элементам A[i][j] для j=0, ..., i-1:

for i in range(n):
    for j in range(0, i):
        A[i][j] = 2

Можно также внешние циклы объединить в один и получить еще одно, более компактное решение:

for i in range(n):
    A[i][i] = 1
for j in range(0, i):
    A[i][j] = 2
for j in range(i + 1, n):
    A[i][j] = 0

А вот такое чисто <<питоновское>> решение использует операцию повторения списков для построения очередной строки списка. i-я строка списка состоит из i чисел 2, затем идет одно число 1, затем идет n-i-1 число 0:

for i in range(n):
    A[i] = [2] * i + [1] + [0] * (n - i - 1)

А цикл можно заменить на генератор:

A = [ [2]*i + [1] + [0]*(n - i - 1) for i in range(n) ]

Вложенные генераторы двумерных массивов

Для создания двумерных массивов можно использовать вложенные генераторы, разместив генератор списка, являющегося строкой, внутри генератора для строк. Например, сделать список из n строк и m столбцов при помощи генератора, создающего список из n элементов, каждый элемент которого является списком из m нулей:

[ [0] * m for i in range(n) ]

Но при этом внутренний список также можно создать при помощи, например, такого генератора: [0 for j in range(m)]. Вложив один генератор в другой получим вложенные генераторы:

[ [0 for j in range(m)] for i in range(n) ]

Но если число 0 заменить на некоторое выражение, зависящее от i (номер строки) и j (номер столбца), то можно получить список, заполненный по некоторой формуле. Например, пусть нужно задать следующий массив (для удобства добавлены дополнительные пробелы между элементами):

0  0  0  0  0  0
0  1  2  3  4  5
0  2  4  6  8 10
0  3  6  9 12 15
0  4  8 12 16 20

В этом массиве n = 5 строк, m = 6 столбцов, и элемент в строке i и столбце j вычисляется по формуле: A[i][j] = i * j . Для создания такого массива можно использовать генератор:

[[ i * j for j in range(m)] for i in range(n)]

Маршруты на плоскости

Все задачи этого раздела будут иметь общее начало:

Дана прямоугольная доска размером n*m (n строк и m столбцов). В левом верхнем углу этой доски находится шахматный король, которого необходимо переместить в правый нижний угол.

Количество маршрутов

Пусть за один ход королю разрешается передвинуться на одну клетку вниз или вправо. Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.

Будем считать, что положение короля задается парой чисел (a, b), где a задает номер строки, а b — номер столбца. Строки нумеруются сверху вниз от 0 до n - 1, а столбцы — слева направо от 0 до m - 1. Таким образом, первоначальное положение короля — клетка (0, 0), а конечное — клетка (n – 1, m – 1).

Пусть W(a, b) — количество маршрутов, ведущих в клетку (a, b) из начальной клетки. Запишем рекуррентное соотношение. В клетку (a, b) можно прийти двумя способами: из клетки (a, b – 1), расположенной слева, и из клетки (a – 1, b), расположенной сверху от данной. Поэтому количество маршрутов, ведущих в клетку (a, b), равно сумме количеств маршрутов, ведущих в клетку слева и сверху от нее. Получили рекуррентное соотношение:

W(a, b) = W(a, b – 1) + W(a – 1, b)

Это соотношение верно при a > 0 и b > 0. Зададим начальные значения: если a = 0, то клетка расположена на верхнем краю доски и прийти в нее можно единственным способом — двигаясь только влево, поэтому W(0, b) = 1 для всех b. Аналогично, W(a, 0) = 1 для всех a.

Создадим массив W для хранения значений функции, заполним первую строку и первый столбец единицами, а затем заполним все остальные элементы массива. Поскольку каждый элемент равен сумме значений, стоящих слева и сверху, заполнять массив W будем по строкам сверху вниз, а каждую строку — слева направо.

В результате такого заполнения получим следующий массив (пример для n = 4, m = 5):

1  1  1  1  1
1  2  3  4  5
1  3  6 10 15
1  4 10 20 35

Как решить задачу нахождения количества маршрутов, если король может передвигаться на одну клетку вниз, вправо или по диагонали вправо-вниз? Решение будет полностью аналогичным, только реккурентная формула для количества маршрутов изменится:

W(a, b) = W(a, b – 1) + W(a – 1, b) + W(a – 1, b – 1)

Полученный в результате заполнения по такой формуле массив W будет выглядеть следующим образом:

1   1   1   1   1
1   3   5   7   9
1   5  13  25  41
1   7  25  63 129

```