Задача №111892. Дружный класс
Кевин учится в школе. В его классе есть мальчики и девочки. Некоторые из них дружат, некоторые - нет. Но если один человек считает второго своим другом, то и второй считает первого своим другом.
Известно, что у каждой девочки \(a\) друзей-девочек и \(b\) друзей-мальчиков, а у каждого мальчика \(c\) друзей-девочек и \(d\) друзей-мальчиков.
Кевин не помнит сколько людей учатся в его классе. Помогите ему найти минимально возможное количество детей, которое удовлетворяет вышеописанным условиям.
Единственная строка входного файла содержит четыре целых числа \(a\), \(b\), \(c\) и \(d\) (\(1 \leq a,b,c,d \leq 50\)).
Выведите класс минимально возможного размера, удовлетворяющий указанным выше условиям.
Первая строка должна содержать два числа: количество девочек \(m\) и количество мальчиков \(n\).
Пусть девочки пронумерованы с \(1\) по \(m\), а мальчики – с \(m + 1\) по \(m + n\).
Каждая из следующих строк должна содержать пару различных целых чисел, описывающих пару друзей. Пары не должны повторяться.
Класс из примера показан ниже:
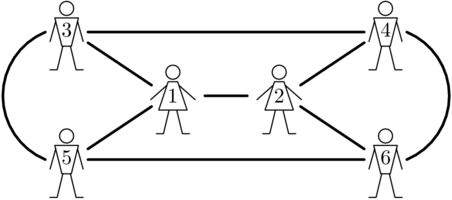
1 2 1 2
2 4 1 2 3 4 4 5 5 6 6 3 1 3 1 4 2 5 2 6