Задача №113897. Эффективное тестирование
Начиная с 20 xx года все организаторы всех школьных олимпиад по программированию договорились проводить соревнования исключительно по интернету, для чего было создано общество с ограниченной ответственностью «Организация онлайн-олимпиад» (ООО «ООО»). Разумеется, такая серьёзная организация не может обойтись без собственной тестирующей системы, поэтому для её создания были наняты эффективные менеджеры, закуплены доски и подготовлена синяя изолента.
Для повышения эффективности процесса тестирования была разработана следующая архитектура. Сначала все m тестов задачи располагаются в порядке от 1 к m в очереди тестирования. Затем модуль планирования последовательно выполняет n действий. Действие i состоит в том, чтобы выбрать отрезок очереди с позиции l i по r i включительно (в нумерации с единицы) и проверить решение на каждом втором тесте на этом отрезке, а именно на тестах на позициях l i , l i + 2, l i + 4, ..., r i очереди (при этом гарантируется, что l i и r i имеют одинаковую чётность). После этого те тесты, на которых было проведено тестирование, удаляются из очереди, а все оставшиеся тесты сдвигаются по очереди таким образом, чтобы пустых мест не осталось. Например, если в очереди находились тесты с исходными номерами 2, 3, 4, 5, 10, 12, 13, 20 и была применена операция с l i = 3 , r i = 7 , то посылка будет протестирована на тестах с позиций 3 , 5 и 7 , которые исходно имели номера 4 , 10 и 13 . После выполнения данной операции очередь тестирования будет состоять из тестов с исходными номерами 2, 3, 5, 12, 20 .
Вам поручено реализовать модуль, который для каждого из n описанных выше действий будет определять минимальный и максимальный номер теста в изначальной нумерации из тех, на которых на этом шаге проверялось решение.
В первой строке входных данных находятся два числа n и m ( 1 ≤ n ≤ 100 000 , 1 ≤ m ≤ 10 18 ) — количество действий модуля планирования и количество тестов в задаче.
В каждой из последующих n строк записаны два целых числа l i и r i ( 1 ≤ l i ≤ r i ≤ m ) — параметры i -го действия модуля планирования. Гарантируется, что перед началом выполнения действия i в очереди тестирования находятся хотя бы r i тестов и что числа l i и r i имеют одинаковую чётность.
Для каждого из n действий модуля планирования выведите два целых числа — минимальный и максимальный номер теста в исходной нумерации из тех, на которых проверялось решение на соответствующем шаге.
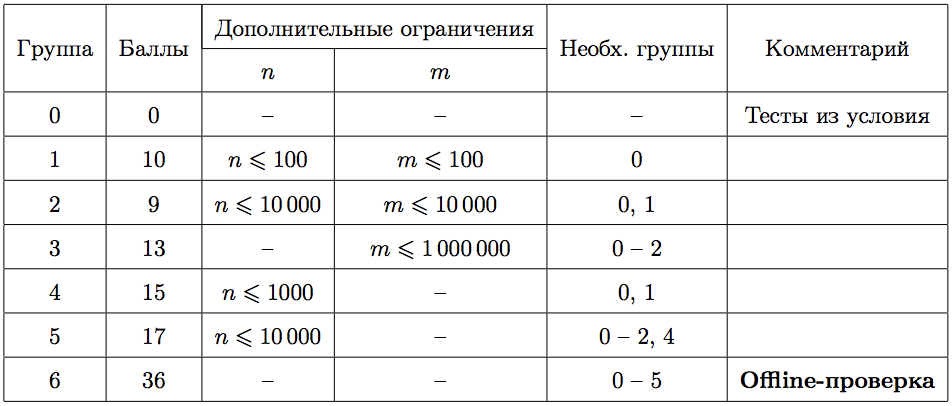
Тесты к этой задаче состоят из семи групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех групп, от которых зависит данная группа. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
Рассмотрим, как изменяется очередь тестирования в первом примере.
- Изначально в очереди тестирования находятся все тесты от 1 до 10 , то есть очередь имеет вид 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 .
- При выполнении первого запроса будут удалены тесты 2, 4, 6, 8 , и очередь примет вид 1, 3, 5, 7, 9, 10 .
- При выполнении второго запроса будут удалены тесты 1 и 5 , очередь примет вид 3, 7, 9, 10 .
2 10 2 8 1 3
2 8 1 5
4 6 1 1 1 1 1 1 2 2
1 1 2 2 3 3 5 5