Задача №113895. Кукушки
Британские учёные решили заняться орнитологией и понаблюдать за жизнью необычных кукушек. Для этого они вырастили дерево и построили на нём n гнёзд, в каждом из которых живёт кукушка. Наблюдение за деревом состоит в том, что в некоторые моменты времени учёные оценивают, можно ли подложить определённое яйцо в гнездо к некоторой кукушке или нет.
Каждое яйцо может вынашиваться только в двух определённых гнёздах. Каждое яйцо задаётся неупорядоченной парой различных чисел ( x , y ) . Яйцо ( x , y ) может вынашиваться в любом из гнёзд x и y и не может вынашиваться в других гнёздах. Обратите внимание, яйцо ( x , y ) не отличается от яйца ( y , x ) .
Теперь опишем процесс подкладывания яйца в имеющиеся гнезда: пусть учёные хотят подложить яйцо ( x , y ) в гнездо x . Если в гнезде x нет яйца, то яйцо ( x , y ) просто остаётся в этом гнезде, и процесс на данном шаге завершается. Если же в гнезде x лежит какое-то яйцо ( x , p ) , то кукушка кладёт яйцо ( x , y ) в данное гнездо, а яйцо ( x , p ) пытается подложить в гнездо p аналогичным образом, и процесс продолжается.
Вам предлагается отвечать на вопросы учёных. Всего есть три типа вопросов:
-
(Теоретический) Закончится ли процесс, если подложить яйцо
(
x
,
y
)
в гнездо
x
? Так как вопрос чисто теоретический, оно
не добавляется
на самом деле, и состояние гнёзд не меняется.
-
(Практический) Закончится ли процесс, если подложить яйцо
(
x
,
y
)
в гнездо
x
? Если процесс закончится, то яйцо
добавляется
в реальности согласно описанному процессу.
- (Теоретический) Сколько существует упорядоченных пар различных чисел ( x , y ) , таких что яйцо ( x , y ) можно подложить в гнездо x c учётом имеющихся в гнёздах яиц? При этом для каждого яйца ответ определяется независимо от других добавляемых яиц.
В первой строке вводятся три целых числа n , m , q , ( 2 ≤ n ≤ 200 000 , 0 ≤ m ≤ n , 1 ≤ q ≤ 600 000 ), где n — количество гнёзд на дереве, m —количество яиц, которые учёные уже положили, q — количество вопросов, которые задают учёные.
В каждой из m последующих строк следуют по два числа x i , y i , означающих, что в гнезде x i лежит яйцо ( x i , y i ) . Гарантируется, что все x i различны и что x i ≠ y i для всех i .
В следующих q строках описаны вопросы учёных. Вопросы даны в том порядке, в котором на них требуется отвечать. Первое число t j в строке описывает тип вопроса.
Если t j = 1 или t j = 2 , то далее идут два различных числа x j и y j , описывающих яйцо, которое фигурирует в соответствующем вопросе.
Если t j = 1 , то яйцо не требуется добавлять в текущую расстановку.
Если t j = 2 , то яйцо требуется добавить, если процесс добавления потребует конечного числа перекладываний.
Если t j = 3 , то требуется определить количество упорядоченных пар ( x , y ) , таких что яйцо ( x , y ) можно добавить в гнездо x с тем, чтобы процесс когда-нибудь завершился. В реальности никакие яйца в расстановку не добавляются.
Для каждого вопроса первого и второго типа выведите единственное слово « Yes » или « No » в зависимости от того, закончится ли процесс перекладывания.
Для каждого запроса третьего типа выведите количество искомых упорядоченных пар.
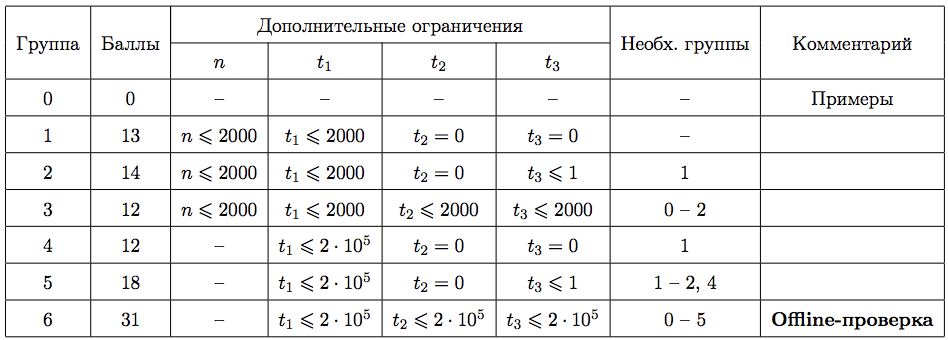
Тесты к этой задаче состоят из шести групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых других групп (смотрите таблицу ниже). Пусть t 1 — количество запросов первого типа, t 2 — количество запросов второго типа, t 3 — количество запросов третьего типа. Offline означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
Изначальное расположение яиц в тесте из условия такое: в первом гнезде лежит яйцо (1, 2) , во втором — (2, 4) , в пятом — (5, 1) , а в третьем и четвёртом яиц нет.
Яйцо (1, 2) добавить можно, несмотря на то что подобное яйцо на дереве уже есть, это приведёт к перекладыванию имеющегося яйца (1, 2) в другое гнездо.
Также в начальную конфигурацию можно добавить любое из 10 яиц, существующих для дерева с пятью гнёздами, и каждое яйцо можно положить в любое из двух гнёзд, ему отвечающих, и для любого из добавляемых яиц и гнёзд это потребует конечное количество шагов. Таким образом, ответ на второй запрос — 20.
В результате следующего запроса яйцо (1, 2) будет добавлено реально, и распределение яиц будет таким: в первом гнезде лежит яйцо (1, 2) , во втором — также (1, 2) , в четвёртом — (2, 4) , в пятом (5, 1) .
Теперь уже можно добавить только яйца (1, 3) , (2, 3) , (4, 3) и (5, 3) , причём по-прежнему любое яйцо можно положить в каждое из двух упомянутых на нём гнёзд, поэтому ответ на запрос — 8.
Яйцо (4, 2) добавить на дерево нельзя, поэтому состояние гнёзд не изменится.
Для добавления яйца (5, 3) понадобится 5 перекладываний яиц, а после этого никакое новое яйцо за конечное количество шагов добавить уже нельзя.
5 3 8 1 2 5 1 2 4 1 1 2 3 2 1 2 3 2 4 2 2 5 3 3 1 4 5
Yes 20 Yes 8 No Yes 0 No