Задача №114041. Машинное обучение
В лаборатории искусственного интеллекта разработали новый метод машинного обучения. В процессе обучения программы используется \(n\) итераций. Каждая итерация заключается в том, что обучаемая программа запускается на некотором обучающем наборе.
Были подготовлены обучающие наборы сложности от \(0\) до \(k\). План обучения задаётся массивом целых чисел \([a_1, a_2, \dots, a_n]\), где \(a_i\) задаёт сложность набора, используемого на \(i\)-й итерации обучения. Для всех \(i\) от \(1\) до \(n\) должно выполняться неравенство \(0 \le a_i \le k\).
Выяснилось, что эффективность плана обучения зависит от битовых представлений сложностей обучающих наборов. Для того, чтобы план был эффективным, необходимо, чтобы для любых двух значений \(i\) и \(j\), где \(1 \leq i \lt 800 j \leq n\), выполнялось \((a_i\,and\,a_j) = a_i\). Напомним, что побитовое «и» (and) двух целых неотрицательных чисел устроено следующим образом: запишем оба числа в двоичной системе счисления, \(i\)-й двоичный разряд результата равен \(1\), если у обоих аргументов он равен \(1\). Например, \((14\,and\,7) = (1110_2\,and\,0111_2) = 110_2 = 6\). Эта операция реализована во всех современных языках программирования, в языках C++, Java и Python она записывается как « & », в Паскале как « and ».
Однако постоянное использование наборов одной сложности не даёт прогресса в обучении. Чтобы этого избежать, для плана обучения должны быть выполнены \(m\) требований следующего вида. Каждое требование задаётся двумя числами \(l_i\) и \(r_i\) и означает, что \(a_{l_i} \ne a_{r_i}\).
Сотрудники лаборатории хотят найти количество эффективных планов, которые удовлетворяют всем требованиям. Так как это число может быть очень большим, нужно найти его остаток от деления на \(10^9 + 7\).
Требуется написать программу, которая по заданным целым числам \(n\) и \(k\), а также \(m\) требованиям вида \(l_i, r_i\) определяет количество эффективных планов, которые удовлетворяют всем требованиям, и выводит остаток от деления этого количества на число \(10^9 + 7\).
Первая строка входных данных содержит три целых числа \(n\), \(m\) и \(k\) — количество итераций обучения, количество требований и максимальную сложность обучающего набора (\(1 \leq n \leq 3 \cdot 10^{5}\), \(0 \le m \le 3\cdot 10^5\), \(0 \leq k \leq 10^{18}\)).
Следующие \(m\) строк описывают требования, \(i\)-я строка содержит два целых числа \(l_i\), \(r_i\), которые означают, что \(a_{l_i} \ne a_{r_i}\) (\(1 \leq l_i \lt r_i \leq n\)). Гарантируется, что все требования различны.
Выведите одно целое число — остаток от деления количества эффективных планов, удовлетворяющих всем требованям, на число \(10^9 + 7\).
Все возможные планы для первого теста: \([0, 0]\), \([0, 1]\), \([0, 2]\), \([0, 3]\), \([1, 1]\), \([1, 3]\), \([2, 2]\), \([2, 3]\), \([3, 3]\).
Для второго теста: \([0, 1, 1], [0, 2, 2]\).
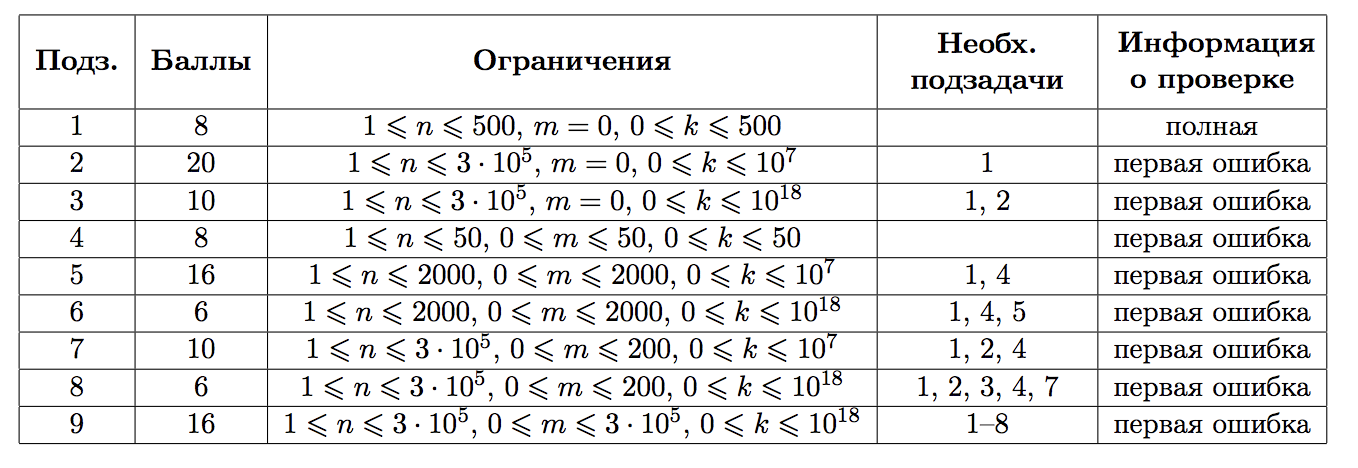
Баллы за каждую подзадачу начисляются только в случае, если все тесты для этой подзадачи и необходимых подзадач успешно пройдены.
2 0 3
9
3 1 2 1 2
2