Задача №114118. Трубка с шариками
В запаянной с обеих сторон трубке, разделённой на n секторов, находятся m шариков. Шарик с номером i изначально находится в секторе с номером a i , причём все шарики находятся в различных секторах. За одну секунду разрешается выполнить одну из двух операций:
- Сдвинуть все шарики на один сектор влево. В этом случае все шарики по очереди, начиная с самого левого, перемещаются на одну позицию влево. Если в момент сдвига шарик i находится в самом левом секторе или в секторе слева расположен шарик, то шарик i не двигается.
- Сдвинуть все шарики на один сектор вправо. В этом случае все шарики по очереди, начиная с самого правого, перемещаются на одну позицию вправо. Если в момент сдвига шарик находится в самом правом секторе или в секторе справа расположен шарик, шарик не двигается.
В k секторах трубки расположены переключатели, изначально находящиеся в выключенном состоянии. Как только в сектор попадает шарик, переключатель переходит во включённое состояние и остаётся в таком состоянии навсегда.
Вася хочет добиться того, чтобы все переключатели оказались включены. Для этого он хочет один раз выполнить одно из следующих действий:
- Выбрать два целых числа x и y ( x , y ≥ 0 ) и выполнить x раз первую операцию, затем y раз вторую операцию.
- Выбрать два целых числа x и y ( x , y ≥ 0 ) и выполнить x раз вторую операцию, затем y раз первую операцию.
За какое минимальное количество операций Вася сможет добиться того, чтобы все переключатели оказались включены?
В первой строке заданы три целых числа n , m и k ( 1 ≤ n ≤ 200 000 , 1 ≤ m ≤ n , 1 ≤ k ≤ n ) — число секторов в трубке, число шариков и переключателей, соответственно.
Во второй строке заданы m различных целых чисел ( 1 ≤ a 1 < a 2 < ... < a m ≤ n ) — сектора, в которых изначально располагаются шарики.
В третьей строке заданы k различных целых чисел ( 1 ≤ b 1 < b 2 < ... < b k ≤ n ) — сектора, в которых располагаются переключатели.
Выведите одно целое число — минимальное количество операций.
В первом примере Васе выгодно совершить первое действие с x = 1, y = 4 , то есть суммарно будет выполнено 5 операций. После движения шарика влево переключатель в секторе 1 окажется во включённом состоянии. Затем Вася сдвинет шарик вправо два раза, после чего переключатель в секторе 3 окажется во включённом состоянии, после чего Вася сдвинет шарик вправо ещё два раза, в результате чего переключатель в секторе 5 окажется во включённом состоянии.
В третьем примере в каждом секторе с переключателем уже есть шарик, поэтому никаких операций выполнять не требуется. Можно считать, что Вася выполнит первое действие с x = 0, y = 0 .
В четвёртом примере Васе выгодно совершить первое действие с x = 1, y = 1 . После движения шариков на один сектор влево, переключатель в секторе 14 окажется включён, а шарики будут находиться на позициях 1 и 14 . После этого Вася сдвинет шарики на 1 сектор вправо, и выключатель на позиции 2 окажется включён.
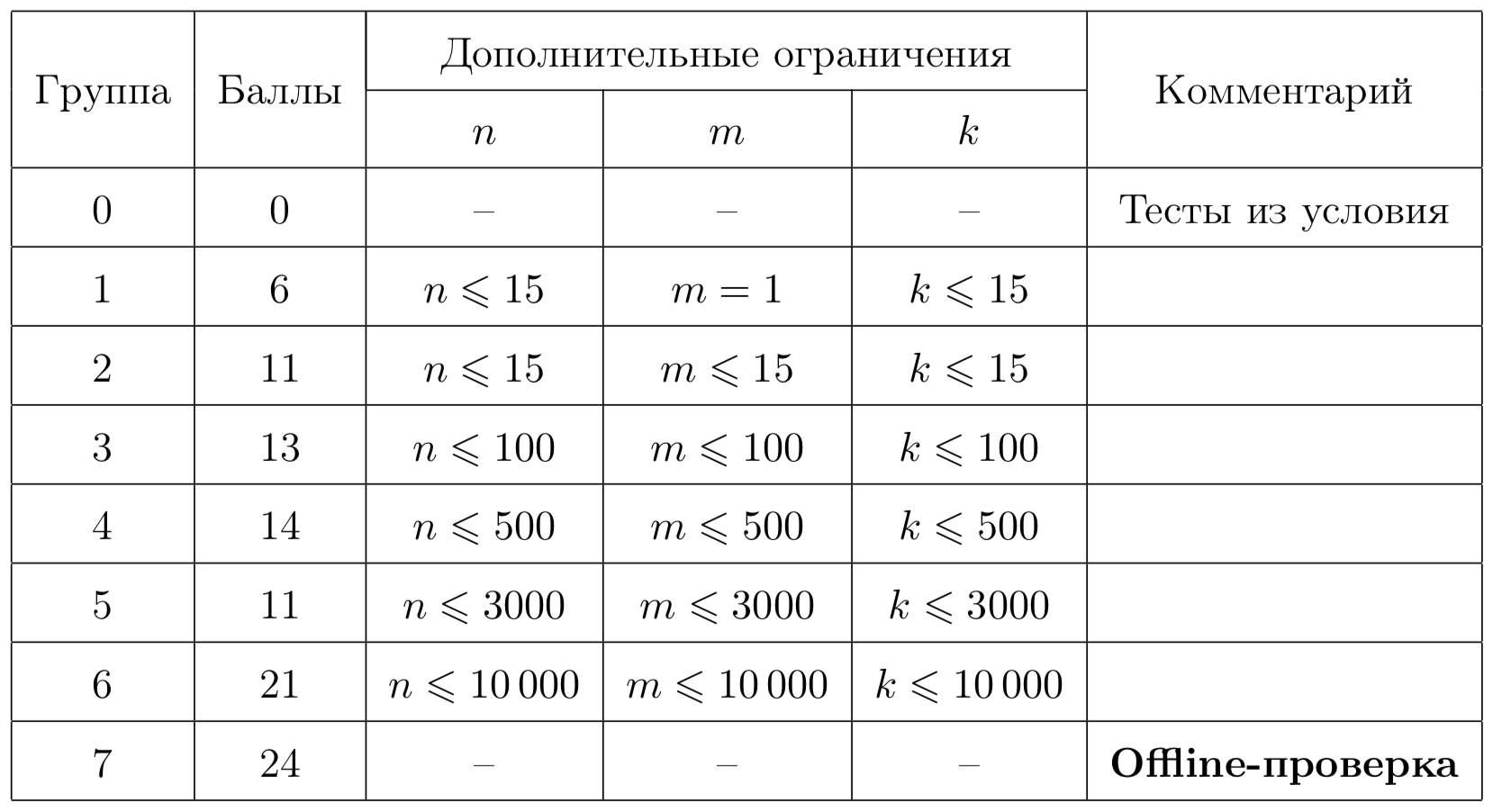
Тесты к этой задаче состоят из семи групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
5 1 3 2 1 3 5
5
10 3 4 1 7 9 2 6 8 10
3
11 5 3 2 5 7 9 11 5 7 9
0
15 2 2 1 15 2 14
2