Задача №114117. Спички детям не игрушка
Лена играется со спичками. Естественный вопрос, посещающий любого школьника, играющего со спичками — а можно ли поджечь спичкой дерево?
Скажем, что дерево — это связный граф без циклов, вершины которого пронумерованы целыми числами \(1, 2, \ldots, n\), в каждой вершине которого также записано некоторое целое число \(p_v\), являющееся приоритетом вершины \(v\). Все приоритеты различны.
Оказывается, что если поджечь дерево, то оно, как и можно было ожидать, сгорит целиком. Однако процесс этот не быстрый. Сначала у дерева сгорает лист ( листом называется вершина, имеющая ровно одного соседа) с минимальным приоритетом, затем сгорает лист с минимальным приоритетом из оставшихся вершин дерева, и так далее. Таким образом, вершины превращаются в листья и сгорают до тех пор, пока от дерева не останется лишь одна вершина, после чего она тоже сгорает.
Лена приготовила дерево из \(n\) вершин и в каждой вершине записала приоритет \(p_v = v\). Лене с одной стороны интересно посмотреть, как горит дерево, но с другой она понимает, что если дерево поджечь, оно исчезнет насовсем. Лена добрая девочка, и деревья ей жалко, так что она хочет ограничиться выяснением ответов на некоторые вопросы про процесс сгорания дерева в уме. Лена хочет ответить на \(q\) вопросов, каждый из которых относится к одному из трёх следующих видов:
- « up \(v\)», присвоить вершине \(v\) приоритет \(1 + \max\{p_1, p_2, \ldots, p_n\}\);
- « when \(v\)», выяснить, какой по счёту сгорит вершина \(v\), если дерево поджечь сейчас;
- « compare \(v\) \(u\)», выяснить, какая из вершин \(v\) и \(u\) сгорит раньше, если дерево поджечь сейчас.
Заметим, что если приоритеты всех вершин сейчас различны, то и после выполнения запроса « up » они тоже останутся различными. Исходно они различны, поэтому в любой момент времени порядок сгорания листьев определён однозначно.
Первая строка содержит два целых числа \(n\) и \(q\) (\(2 \le n \le 200\,000\), \(1 \le q \le 200\,000\)) — количество вершин дерева и количество вопросов.
В \(i\)-й из следующих \(n - 1\) строк находятся два целых числа \(v_i\), \(u_i\) (\(1 \le v_i, u_i \le n\)), задающие концы \(i\)-го ребра дерева.
Каждая из оставшихся \(q\) строк содержит операцию одного из трёх типов.
- « up \(v\)» (\(1 \le v \le n\)) — присвоить новый приоритет вершине \(v\);
- « when \(v\)» (\(1 \le v \le n\)) — определить момент сгорания вершины \(v\) для текущего дерева;
- « compare \(v\) \(u\)» (\(1 \le v, u \le n\), \(v \ne u\)) — определить, какая из вершин \(v\) и \(u\) сгорит раньше для текущего дерева.
Гарантируется, что среди запросов хотя бы один имеет тип « when » или « compare ».
Для каждого запроса типа « when » нужно вывести одно целое число от \(1\) до \(n\) — момент времени, когда сгорит вершина \(v\).
Для запроса типа « compare » выведите \(v\) или \(u\), в зависимости от того, какая вершина сгорит раньше.
В первом примере процесс сгорания исходного дерева проиллюстрирован на картинке:
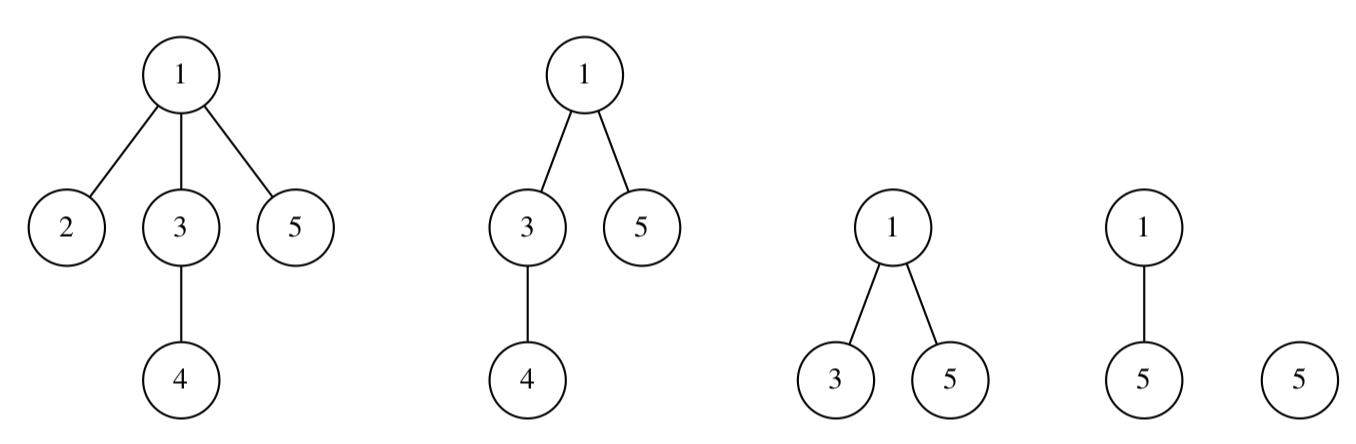
В частности, порядок сгорания вершин следующий: [2, 4, 3, 1, 5] Во втором примере после применения операции «up» порядок сгорания вершин станет следующим: [2, 4, 3, 5, 1]
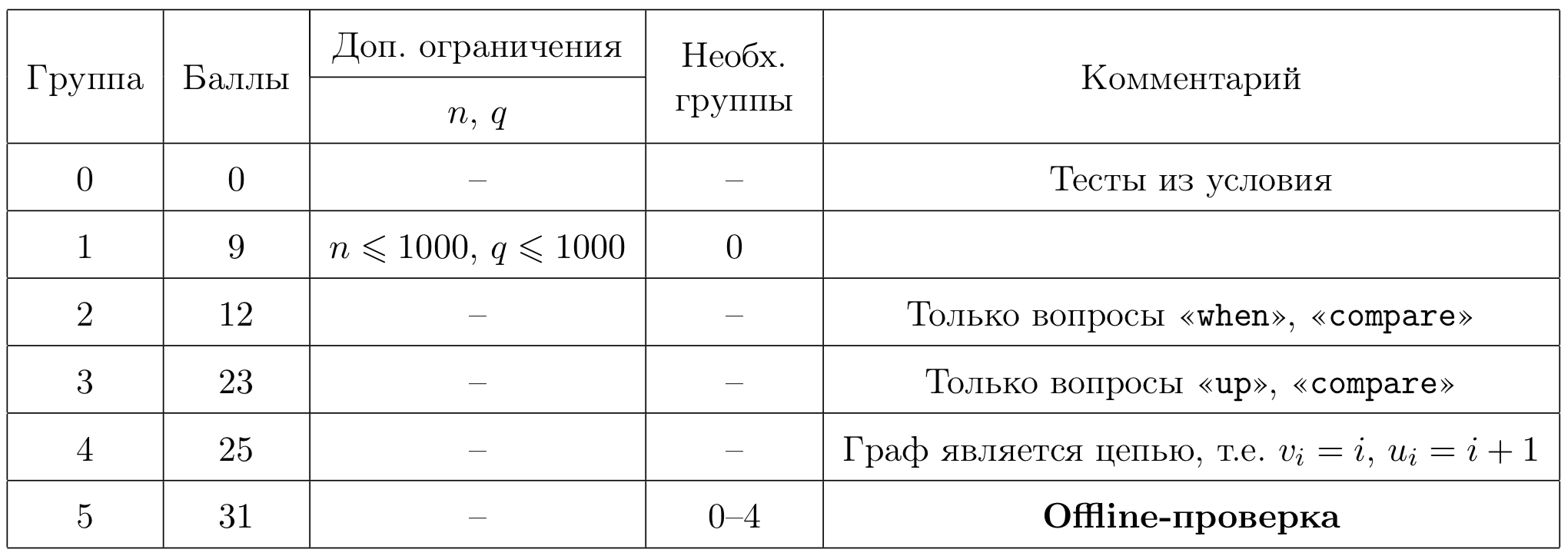
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов необходимых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
5 7 1 5 1 2 1 3 4 3 when 1 when 2 when 3 when 4 when 5 compare 2 3 compare 3 4
4 1 3 2 5 2 4
5 5 1 5 1 2 1 3 4 3 up 1 compare 2 4 compare 4 3 compare 3 1 compare 1 5
2 4 3 5