Задача №114155. Обгон запрещён
Сегодня вечером супергерой Ватман планирует навестить свою любимую бабушку. Так как он вовремя не продлил лицензию на полёты, ему придётся ехать на ватмобиле сквозь Готэмские пробки. Необходимо закончить дела и добраться до бабушки как можно быстрее, ведь пирожки уже остывают!
Часть пути Ватману предстоит проехать по дороге, имеющей лишь одну полосу в каждом из двух возможных направлений движения. В рамках данной задачи дорогу можно считать бесконечной прямой. На обеих полосах движения в совокупности находятся N автомобилей, про каждый из которых известно его начальное положение p i и его постоянная скорость v i . Таким образом, координата i -го автомобиля в момент времени t будет равняться x i ( t ) = p i + v i · t . Однако, данная формула справедлива только до тех пор, пока этот автомобиль не догонит другой, движущийся в том же направлении (а значит, и по той же полосе), но медленнее. Так как обгон на данном участке дороги запрещён, то, догнав более медленный автомобиль, более быстрый вынужден снизить скорость и двигаться сразу за ним всё оставшееся время.
Ватман эгоистично полагает, что достаточно часто думает о судьбах простых людей, чтобы позволить себе пренебречь некоторыми правилами дорожного движения. Сегодня вечером он планирует обгонять другие автомобили по встречной полосе, но, как и любой нормальный супергерой, Ватман стремится избегать аварийных ситуаций. В связи с этим он совершает обгон, только если ближайший двигающийся навстречу автомобиль находится на безопасном расстоянии, обозначаемом в данной задаче как d .
Планы Ватмана постоянно меняются, он пока не знает, когда именно поедет в гости к бабушке, какой маршрут выберет, на каком из многочисленных ватмобилей поедет и какую дистанцию для обгона будет считать безопасной. Поэтому он попросил вас рассчитать минимальное время поездки по данной дороге для Q различных значений параметров задачи.
Длиной автомобилей следует пренебречь, то есть можно считать их точками на прямой. Также следует считать, что как только более быстрая машина догоняет более медленную, она двигается за ней на расстоянии 0 . Ватман может совершить обгон, если на встречной полосе в направлении движения ватмобиля отсутствуют встречные машины на расстоянии как минимум d . Машины, находящиеся на встречной полосе и имеющие такую же координату как и ватмобиль, помехой для обгона не являются. Начав обгон, Ватман совершает его мгновенно и тут же возвращается на исходную полосу.
Поскольку любые вычисления, связанные с вещественными числами, сопряжены с неизбежной погрешностью, жюри гарантирует вам, что Ватману никогда не придётся принимать решение об обгоне, основываясь на сравнении очень близких друг к другу чисел. Это значит следующее: изменение d на 0 ≤ eps ≤ 0.001 в любую сторону не повлияет на правильный ответ к задаче.
В первой строке ввода содержатся два целых числа N и Q — количество автомобилей на дороге и запросов Ватмана соответственно ( 0 ≤ N ≤ 10 000 , 1 ≤ Q ≤ 5 000 ).
В каждой из следующих N строк содержатся по два целых числа p i и v i , описывающих начальное положение и начальную скорость i -го автомобиля соответственно ( | p i | ≤ 100 000 , | v i | ≤ 100 000 , v i ≠ 0 ). Машины с положительным значением v i двигаются по одной полосе, а с отрицательным — по другой. Гарантируется, что все p i различны.
Далее следуют Q строк с описаниями запросов. Каждый из них задаётся пятью целыми числами t i , a i , b i , v i , d i — соответственно, момент времени, в который Ватман планирует выехать на дорогу, начальная и конечная точки его маршрута, максимальная скорость ватмобиля и минимальная дистанция до встречного автомобиля, которую Ватман считает безопасной для обгона ( | a i |, | b i | ≤ 100 000 , 0 < | v i | < 100 000 , 0 ≤ t i , d i ≤ 100 000 ). Гарантируется, что a i ≠ b i , и что в момент времени t i никакая машина, кроме ватмобиля, не имеет координату a i . Также гарантируется, что v i > 0 тогда и только тогда, когда b i > a i .
Для каждого запроса выведите в отдельной строке одно число — минимальное время, за которое Ватман может успеть добраться из начальной точки в конечную. Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность не будет превосходить 10 - 6 .
Более формально, пусть ваш ответ равен
A
, а ответ жюри —
B
. Проверяющая программа будет считать ваш ответ правильным, если
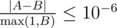 .
.
В первом примере никто не помешает Ватману совершить обгон, и он доедет за минимально возможное для своей максимальной скорости время.
Во втором примере Ватман догонит первую машину в точке с координатой 70 , в этот момент вторая машина будет иметь координату 100 , то есть обгонять будет уже слишком поздно. Ватману придётся две секунды ехать медленнее, пока вторая машина не проедет мимо.
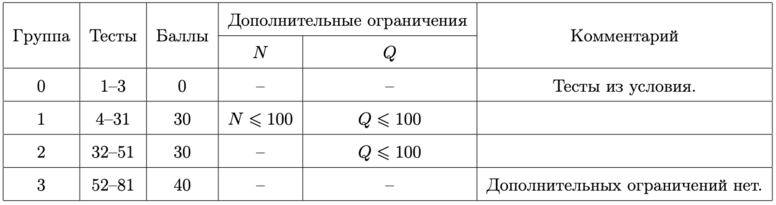
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
1 1 10 10 0 0 100 20 10
5.0000000000
2 1 20 5 200 -10 4 10 100 10 40
10.0000000000
6 3 20 1 10 10 5 100 80 -1 90 -10 95 -100 0 0 100 10 1 0 0 100 10 100 0 100 0 -10 100
10.0000000000 35.0000000000 35.0000000000