Задача №114146. Рассадка
Олимпиада всегда приносит много хлопот для жюри и оргкомитета, и очный тур Открытой олимпиады не является исключением из этого правила. Пока пишутся условия, готовятся тесты, создаются разборы и настраиваются компьютеры, очень легко забыть правильно рассадить участников олимпиады по аудиториям.
В этот раз, в целях рационального использования рабочих мест, оргкомитет олимпиады поставил перед собой задачу — создать компактную рассадку школьников по M имеющимся аудиториям. Рассадка называется компактной, если для любых двух различных аудиторий количества детей в них отличаются не более чем на один.
В жюри олимпиады имеется человек с экстрасенсорными способностями, который может очень точно предсказывать результаты будущих соревнований по программированию. Хотя результаты заочного тура ещё не известны, он без труда определил, что на очный тур пройдут ученики из K школ. Кроме того, было предсказано, что из i -й школы (1 ≤ i ≤ K ) пройдёт в точности n i учеников. Хотя отношение большей части оргкомитета к подобным прогнозам зачастую скептическое, они имеют странное свойство сбываться, поэтому вам предлагается на всякий случай вычислить максимально возможное количество участников, которые попадут в одну аудиторию при компактной рассадке, если предсказание окажется верным.
В первой строке ввода находятся два целых числа M и K — количество аудиторий и количество школ, участвующих в очном туре олимпиады согласно предсказанию ( 1 ≤ M ≤ 10 9 , 1 ≤ K ≤ 100 000 ).
В следующей строке находятся K чисел n i , разделённых пробелами, i -е из которых обозначает, сколько участников предположительно приедет из i -й школы ( 1 ≤ n i ≤ 10 9 ).
Выведите одно число — максимальное количество людей в аудитории при компактной рассадке.
В первом тесте существует только одна компактная рассадка — в каждую из аудиторий рассадить по 7 человек.
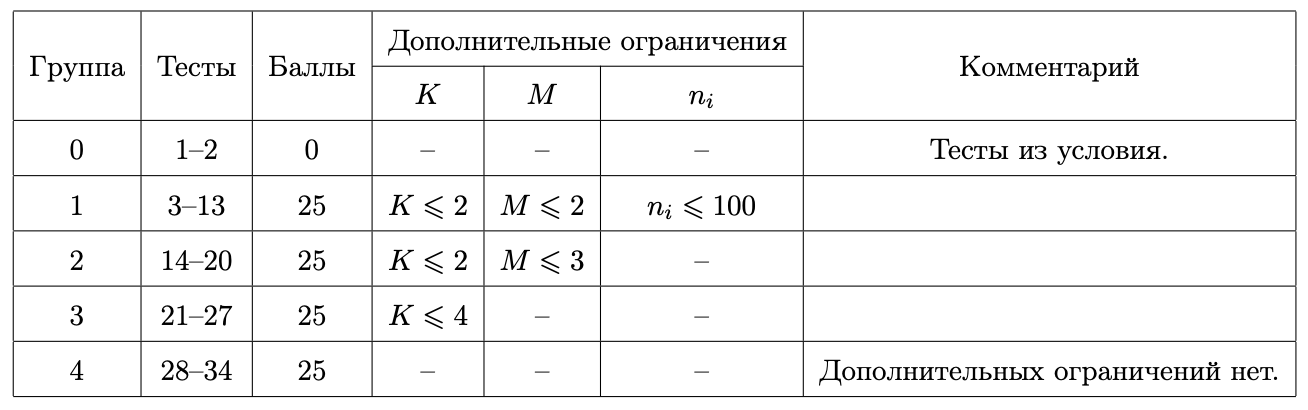
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
2 2 5 9
7
1 2 20 10
30