Задача №115016. Перевернутые родословные
Участникам, использующим язык Python3 , рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3 .
Учёный Иван Иванович изучает перевёрнутые родословные. Перевёрнутая родословная представляет собой набор людей, про каждого из которых известны либо оба его родителя, либо не известен ни один родитель. Кроме того, известно, что у всех людей из родословной есть ровно один ребёнок, кроме одного человека, у которого детей вовсе нет. Поэтому, если пронумеровать людей целыми числами от \(1\) до \(n\), то можно обозначить за \(s_i\) номер ребёнка человека с номером \(i\) и сказать, что \(s_i = 0\) в случае, если у человека с номером \(i\) детей нет.
Будем считать, что человек \(a\) входит в родословную человека \(b\), если либо \(a = b\), либо если у \(b\) известны родители, и \(a\) входит в родословную одного из родителей \(b\).
Будем считать, что произошёл перекос родословной с участием некоторого человека, если известны оба его родителя и количество людей в родословной одного из его родителей хотя бы вдвое больше, чем количество людей в родословной второго родителя.
Иван Иванович посчитал количество перекосов родословной и получил число \(k\), но, конечно же, он делал это вручную и мог ошибиться. Помогите проверить Ивану Ивановичу его вычисления: по числам \(n\) и \(k\) скажите, существует ли родословная из \(n\) людей с \(k\) перекосами, и если существует, то приведите пример подобной родословной.
В единственной строке заданы два целых числа \(n\) и \(k\) (\(1 \leq n \leq 100\,000\), \(0 \leq k \leq n\)) — количество людей в родословной и количество перекосов в ней.
В первой строке выведите «YES» (без кавычек), если существует родословная с \(n\) людьми и \(k\) перекосами, и «NO» (без кавычек) в противном случае.
Если требуемая родословная существует, то во второй строке выведите \(n\) целых чисел \(s_1, s_2, \ldots, s_n\) (\(0 \leq s_i \leq n\)), задающих номера детей каждого из \(n\) человек в родословной. Если искомых родословных несколько, выведите любую.
В первом примере подойдет единственная родословная, которую можно составить из трёх человек (человек и два его родителя).
Во втором примере подойдет следующая родословная:
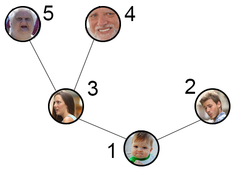
В этом случае в родословную человека \(1\) входят пять человек (люди \(1\), \(2\), \(3\), \(4\), \(5\)), в родословную человека \(2\) входит один человек (только \(2\)), в родословную человека \(3\) входят три человека (\(3\), \(4\), \(5\)), в родословную человека \(4\) входит один человек (только \(4\)) и в родословную человека \(5\) входит один человек (только \(5\)). В этом случае происходит перекос родословной в человеке \(1\).
В третьем примере можно показать, что не существует родословной из трёх людей с двумя перекосами.
Тесты к этой задаче состоят из пяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.
| Группа | Баллы | \(n\) | Комментарий |
| \(0\) | \(0\) | — | Тесты из условия |
| \(1\) | \(11\) | \(n \le 10\) | — |
| \(2\) | \(19\) | \(n \le 100\) | — |
| \(3\) | \(17\) | \(n \le 300\) | — |
| \(4\) | \(22\) | \(n \le 1000\) | — |
| \(5\) | \(31\) | — | — |
3 0
YES 0 1 1
5 1
YES 0 1 1 3 3
3 2
NO