Открытая олимпиада школьников по программированию

Задача №115191. Доска улик

Володя мечтает стать детективом. Поэтому Володя нередко читает книги, в которых рассказывается об невероятных историях раскрытия преступных группировок. Изучая очередное дело Володя наткнулся на интересные подробности следствия.

Всего в деле было $n$ подозреваемых. На доске улик были изображены все $n$ подозреваемых. Изначально у детективов не было никаких связей между подозреваемыми.

Однако в ходе расследования поочерёдно возникали новые улики. Каждая улика связывала двух подозреваемых, причём ранее эти подозреваемые не имели никакой связи друг с другом, даже косвенной, через несколько других подозреваемых.

Рассмотрим, что происходило, когда у детективов возникала улика, указывающая на связь между подозреваемыми $A$ и $B$. Кроме имён подозреваемых, у каждой улики было три параметра: $c_A$ — сила доказательства против $A$, $c_B$ — сила доказательства против $B$, а также $w_{AB}$ — общая сила улики. По естественным соображениям сила улики не могла превышать суммарную силу доказательств против $A$ и $B$, то есть для каждой улики обязательно выполнялось $w_{AB} \leq c_A + c_B$. Получив такую улику, детективы проводили на доске ребро (линию) между изображениями $A$ и $B$, назначая этому ребру вес равный силе улики, $w_{AB}$. А также на изображение подозреваемого $A$ наклеивался стикер с числом $c_A$, а на $B$ наклеивался стикер с числом $c_B$. Причём, если на изображении уже были другие стикеры, новый стикер наклеивался поверх старых.

Дело было раскрыто ровно в тот момент, когда все подозреваемые оказались связаны, через $n-1$ улику. После раскрытия преступления, доска в неизменном виде была помещена в музей.

Вдохновлённый таким подходом Володя посетил музей, в котором сохранилась доска с этого расследования, и подробно изучил ее. Володя увидел, что изображение подозреваемого $v$ содержало стикеры с числами $c_{v,1}, \ldots, c_{v,deg_v}$ пронумерованных от верхнего к нижнему . Здесь $deg_v$ обозначает количество улик, связанных с подозреваемым $v$. Также Володя запомнил, что $i$-я улика соединяла подозреваемых $a_i$ и $b_i$ и имела силу доказательства $w_i$, однако улики были пронумерованы произвольным образом и их номера не обязательно соответствовали тому порядку, в котором они появлялись во время следствия.

Из-за путаницы с номерами улик, информация на доске не помогала воссоздать полную картину следствия. Чтобы полностью восстановить историю дела, Володе необходимо восстановить любой возможный хронологический порядок, в котором улики могли появляться у детективов. Но эта задача для него непосильно трудна. Помогите ему! Если есть несколько возможных вариантов восстановления, подойдёт любой из них. Также возможна ситуация, что музей подделал часть информации, и подходящего порядка не существует.

Входные данные

В первой строке входных данных даны два целых числа $n$ и $g$ ($2 \le n \le 200\,000$, $0 \le g \le 9$) — количество подозреваемых в деле и номер группы тестов.

В следующих $n - 1$ строках описываются улики. В $i$-й строке даны три целых числа $a_i$, $b_i$ и $w_i$ ($1 \le a_i, b_i \le n$, $1 \le w_i \le 10^9$, $a_i \neq b_i$) — номера подозреваемых, которых связывает $i$-я улика, и общая сила $i$-й улики. Гарантируется, что улики связывают всех подозреваемых между собой.

В следующих $n$ строках описываются числа, написанные на стикерах. В $i$-й строке дано $deg_i$ целых чисел $c_{i, 1}, \ldots, c_{i, deg_i}$ ($0 \le c_{i, j} \le 10^9$) — числа написанные на стикерах на изображении $i$-го подозреваемого от верхнего к нижнему. Напомним, что $deg_i$ равняется количеству улик, связанных с подозреваемым $i$.

Выходные данные

Если подходящего под условия задачи хронологического порядка восстановления улик не существует, в единственной строке выведите « No » (без кавычек).

Иначе, в первой строке выведите « Yes » (без кавычек). Во второй строке выведите $n - 1$ чисел — подходящий хронологический порядок возникновения улик. Улики пронумерованы от $1$ до $n-1$ в таком же порядке, как они заданы во входных данных. Если возможных порядков несколько, выведите любой из них.

Примечание

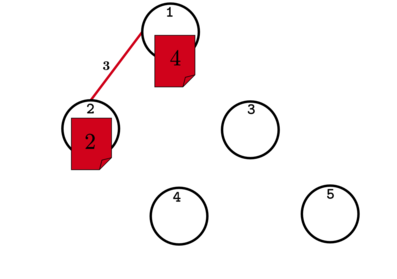
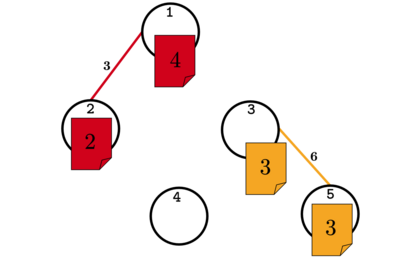
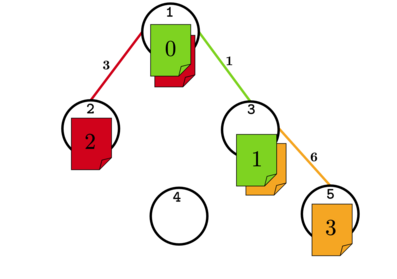
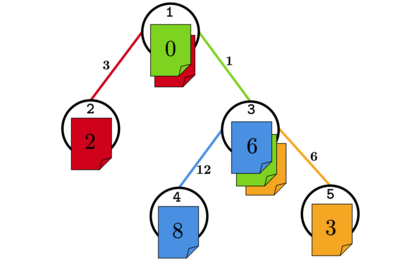
В первом тесте из условия один из возможных порядков — $[1, 4, 2, 3]$. Первая, в хронологическом порядке, улика связывает $A = 1$ и $B = 2$, $c_A = 4, c_B = 2, w_{AB} = 3$, $3 \leq 2 + 4$ — улика корректная. Вторая, в хронологическим порядке, улика связывает $A = 3$ и $B = 5$, $c_A = 3, c_B = 3, w_{AB} = 6$, $6 \leq 3 + 3$ — улика корректная. Третья, в хронологическом порядке, улика связывает $A = 1$ и $B = 3$, $c_A = 0, c_B = 1, w_{AB} = 1$, $1 \leq 0 + 1$ — улика корректная. Четвёртая, в хронологическом порядке, улика связывает $A = 3$ и $B = 4$, $c_A = 6, c_B = 8, w_{AB} = 12$, $12 \leq 6 + 8$ – улика корректная. Для лучшего понимания смотрите иллюстрацию.

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Система оценки

Тесты к этой задаче состоят из девяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.

		Доп. ограничения
Группа	Баллы	$n$	$a_i, b_i, c_i, w_i$	Необх. группы	Комментарий
0	0	–	–	–	Тесты из условия.
1	10	$n \le 10$	–	0	–
2	15	–	$a_i = i, b_i = i+1$ для всех $i$	–	–
3	8	–	$a_i = 1, b_i = i+1$ для всех $i$	–	–
4	9	–	$a_i \leq 2, b_i = i+1$ для всех $i$	3	–
5	7	$n \le 1000$	$c_{i,1} \leq c_{i,2} \leq \ldots \leq c_{i, deg_i}$ для всех $i$	–	–
6	7	$n \le 1000$	$c_{i, j} = 0$ для всех $1 \le i \le n$ и $j \geq 2$	–	–
7	17	–	$\displaystyle\sum_{v=1}^{n} \displaystyle\sum_{i=1}^{deg_v} c_{v,i} = \displaystyle\sum_{i=1}^{n-1} w_i$	–	–
8	16	$n \le 1000$	–	0, 1, 5, 6	–
9	11	–	–	0 – 8	Offline-проверка.

Примеры

Входные данные

Выходные данные

Yes
1 4 2 3

Входные данные

Выходные данные

Yes
1 2 3 5 4 6

Входные данные

Выходные данные

No

Сдать: для сдачи задач необходимо войти в систему