Задача №115190. Нарисуй ломаные
Это интерактивная задача.
Вам даны \(n\) точек \(A_i = (x_i, y_i)\) на плоскости. Известно, что все \(x_i\) различны и все \(y_i\) различны.
Ваша задача — рисовать на плоскости ломаные линии, соединяющие эти \(n\) точек.
Ломаная линия задается перестановкой \(p_1, p_2, \ldots, p_n\) чисел от \(1\) до \(n\). Ломаная линия состоит из \(n-1\) отрезков, первый отрезок соединяет точки \(A_{p_1}\) и \(A_{p_2}\), второй отрезок соединяет точки \(A_{p_2}\) и \(A_{p_3}\), \(\ldots\), последний отрезок соединяет точки \(A_{p_{n-1}}\) и \(A_{p_n}\). Обратите внимание, что отрезки могут пересекаться.
Остротой ломаной линии назовем количество индексов \(2 \leq i \leq n - 1\), таких что угол \(\angle A_{p_{i-1}} A_{p_i} A_{p_{i+1}}\) острый, то есть строго меньше \(90^{\circ}\).
Вам нужно решить четыре задачи:
- Найти любую ломаную линию, которая имеет максимальную возможную остроту.
- Дано некоторое целое число \(c\). Найти любую ломаную линию, острота которой \(\leq c\).
-
Дано некоторое целое число \(c\).
Ответить на \(q\) запросов, каждый задается единственным целым числом \(k_i\) (\(c \leq k_i \leq n - c\)). В \(i\)-м запросе нужно построить ломаную линию, которая имеет остроту ровно \(k_i\).
-
Дано некоторое целое число \(c\).
Для каждого \(k\) от \(c\) до \(n - c\) построить ломаную \(p^{(k)}\), имеющую остроту ровно \(k\). В качестве ответа предоставить \(n - 2c + 1\) чисел \(\text{hash}\left(p^{(c)}\right), \text{hash}\left(p^{(c+1)}\right), \ldots, \text{hash}\left(p^{(n-c)}\right)\), где \(hash(p) = \left( \sum\limits_{i=1}^{n} p_i b^{i-1} \right) \bmod m\) — полиномиальный хеш перестановки \(p\) с параметрами \(b = 10^6 + 3\) и \(m = 10^9 + 7\).
Затем нужно ответить на \(q\) запросов, каждый задается единственным целым числом \(k_i\) (\(c \leq k_i \leq n - c\)). В \(i\)-м запросе нужно предоставить ломаную \(p^{(k_i)}\). Будет проверено, что острота этой ломаной ровно \(k_i\) и ее хеш равен предоставленному ранее значению \(\text{hash}\left(p^{(k_i)}\right)\).
Обратите внимание, что запросы будут появляться после получения хешей.
Гарантируется, что в данных ограничениях ответ всегда существует.
В первой строке находятся два целых числа \(\text{task}\), \(\text{group}\) (\(1 \leq \text{task} \leq 4\), \(0 \leq \text{group} \leq 21\)) — номер задачи, которую надо решить в этом тесте и номер группы теста.
Во второй строке находится единственное целое число \(n\) (\(3 \leq n \leq 80\,000\)) — количество точек на плоскости.
В каждой из следующих \(n\) строк находятся два целых числа \(x_i\), \(y_i\) (\(|x_i|, |y_i| \leq 10^9\)) — координаты точек. Гарантируется, что все \(x_i\) различны и все \(y_i\) различны.
Если \(\text{task} = 1\), то на этом входные данные заканчиваются и вы должны вывести любую перестановку, острота которой максимально возможная. На этом взаимодействие завершается.
Если \(\text{task} \neq 1\), то в следующей строке находится единственное целое число \(c\) (\(2 \leq c \leq \frac{n}{2}\)).
Если \(\text{task} = 2\), то на этом входные данные заканчиваются и вы должны вывести любую перестановку, острота которой \(\leq c\). На этом взаимодействие завершается.
Если \(\text{task} = 4\), то ваше решение должно вывести \(n - 2c + 1\) целых чисел \(\text{hash}\left(p^{(c)}\right), \text{hash}\left(p^{(c+1)}\right), \ldots, \text{hash}\left(p^{(n-c)}\right)\), где \(0 \leq \text{hash}\left(p^{(i)}\right) < 10^9 + 7\). Обратите внимание, что этого не надо делать, если \(\text{task} = 3\).
Дальнейшее взаимодействие происходит только при \(\text{task} = 3\) или \(\text{task} = 4\).
В следующей строке находится единственное целое число \(q\) (\(1 \leq q \leq 50\)) — количество запросов.
Затем \(q\) раз в очередной строке появляется запрос \(k_i\) (\(c \leq k_i \leq n - c\)). В качестве ответа вы должны в отдельной строке вывести перестановку. Острота этой перестановки должна быть ровно \(k_i\). Если \(\text{task} = 4\), то хеш этой перестановки должен совпадать с предоставленным ранее хешом.
Поскольку задача интерактивная, после вывода каждой строки не забывайте выводить символ перевода строки и сбрасывать буфер выходного потока.
Тесты к этой задаче состоят из двадцать одной группы. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов необходимых для нее групп.
| Ограничения | |||||||
| Группа | Баллы | \(\text{task}\) | \(n\) | \(c\) | Доп. ограничения | Необх. группы | Комментарий |
| 0 | 0 | – | – | – | – | – | Тесты из условия. |
| 1 | 8 | \(1\) | \(n \leq 20\,000\) | – | \(x_i \lt x_{i+1}\), \(y_i \lt y_{i+1}\) | – | |
| 2 | 6 | \(1\) | \(n \leq 10\) | – | точки случайные | – | |
| 3 | 5 | \(1\) | \(n \leq 1000\) | – | точки случайные | 2 | |
| 4 | 5 | \(1\) | \(n \leq 20\,000\) | – | точки случайные | 2 – 3 | |
| 5 | 6 | \(1\) | \(n \leq 20\,000\) | – | – | 1 – 4 | |
| 6 | 17 | \(2\) | \(n = 80\,000\) | \(c = 800\) | – | – | |
| 7 | 7 | \(3\) | \(n = 80\,000\) | \(c = 800\) | \(x_i \lt x_{i+1}\), \(y_i \lt y_{i+1}\) | – | |
| 8 | 4 | \(3\) | \(n = 50\) | \(c = 25\) | точки случайные | – | |
| 9 | 4 | \(3\) | \(n = 200\) | \(c = 80\) | точки случайные | – | |
| 10 | 4 | \(3\) | \(n = 1000\) | \(c = 300\) | точки случайные | – | |
| 11 | 3 | \(3\) | \(n = 5000\) | \(c = 600\) | точки случайные | – | |
| 12 | 3 | \(3\) | \(n = 80\,000\) | \(c = 35\,000\) | точки случайные | – | |
| 13 | 3 | \(3\) | \(n = 80\,000\) | \(c = 5000\) | точки случайные | 12 | |
| 14 | 3 | \(3\) | \(n = 80\,000\) | \(c = 2000\) | – | 12 – 13 | |
| 15 | 2 | \(3\) | \(n = 80\,000\) | \(c = 800\) | – | 7, 12 – 14 | |
| 16 | 6 | \(4\) | \(n = 80\,000\) | \(c = 800\) | \(x_i \lt x_{i+1}\), \(y_i \lt y_{i+1}\) | – | |
| 17 | 3 | \(4\) | \(n = 5000\) | \(c = 600\) | точки случайные | – | |
| 18 | 3 | \(4\) | \(n = 80\,000\) | \(c = 35\,000\) | точки случайные | – | |
| 19 | 3 | \(4\) | \(n = 80\,000\) | \(c = 5000\) | точки случайные | 18 | |
| 20 | 3 | \(4\) | \(n = 80\,000\) | \(c = 2000\) | – | 18 – 19 | |
| 21 | 2 | \(4\) | \(n = 80\,000\) | \(c = 800\) | – | 16, 18 – 20 | |
В тех группах, в которых указано, что точки случайные, все координаты всех точек \(x_i\), \(y_i\) сгенерированы случайно равновероятно на отрезке \([-10^9, 10^9]\).
На всех картинках двумя дугами обозначены острые углы, одной дугой обозначены не острые углы.
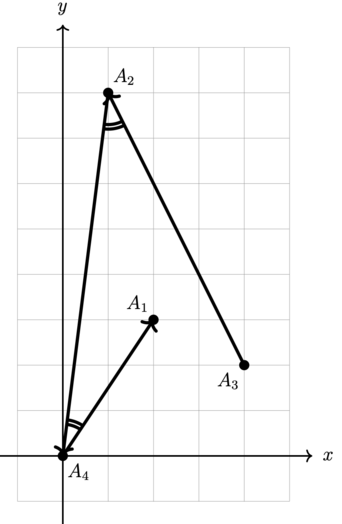
В первом тесте из условия оба угла ломаной острые, поэтому ломаная имеет максимально возможную остроту \(2\).
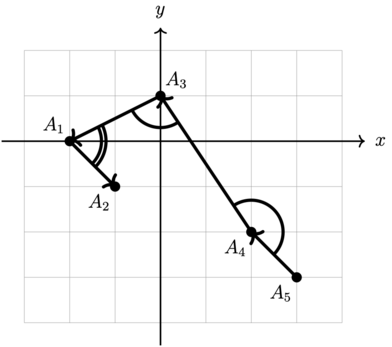
Во втором тесте из условия острота равна \(1\), она \(\leq 2\), поэтому ломаная подходит.
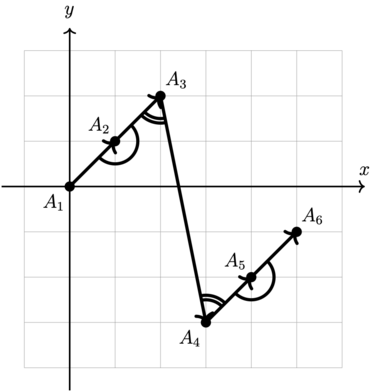
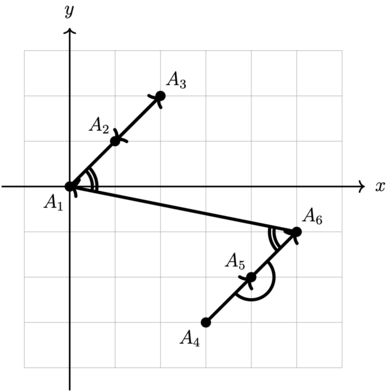
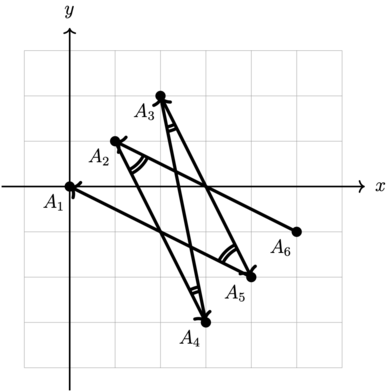
В третьем тесте из условия мы строим ломаные, которые имеют остроту \(2\), \(3\), \(4\).
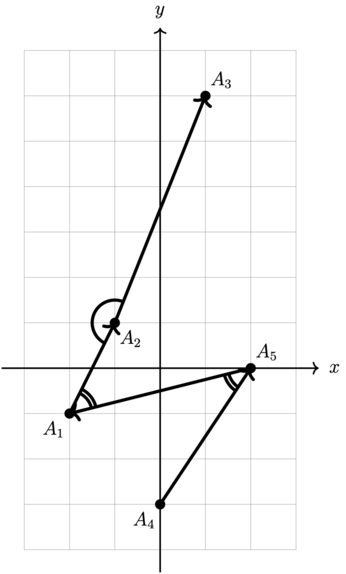
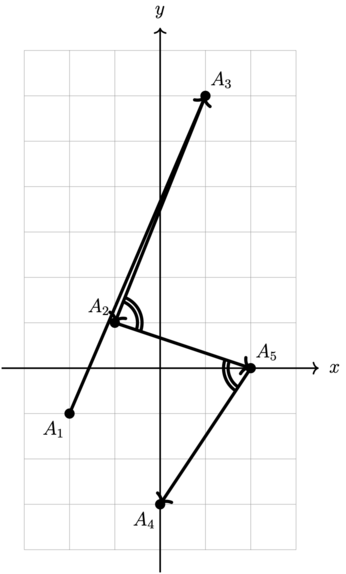
В четвертом тесте из условия мы последовательно строим ломаные, которые имеют остроту \(2\), \(3\). При этом заранее были предоставлены хеши ломаных, которые совпадают с хешами приведенных далее ломаных.
1 0 4 2 3 1 8 4 2 0 0
2
2 0 5 -2 0 -1 -1 0 1 2 -2 3 -3 2
1
3 0 6 0 0 1 1 2 2 3 -3 4 -2 5 -1 2 3 2 3 4
2 495950387 3 209421083 4 342006638
4 0 5 -2 -1 -1 1 1 6 0 -3 2 0 2 2 2 3
780155088 554707211 2 780155088 3 554707211