Задача №115192. Больше подарков хороших и разных
Организаторы Закрытой олимпиады школьников по программированию решили подготовить подарки для участников олимпиады. Всего было заказано \(k\) одинаковых коробок с подарками, каждая коробка содержит стопку из \(n\) подарков. Вверху каждой стопки лежит подарок типа \(a_1\), под ним подарок типа \(a_2\), и так далее, внизу стопки лежит подарок типа \(a_n\).
Раздача подарков будет происходить следующим образом: сначала будут отдаваться подарки из первой стопки сверху вниз. После того, как в первой стопке не останется подарков, будут отдаваться подарки из второй стопки сверху вниз, и так далее, в конце будут отдаваться подарки из \(k\)-й стопки.
Участнику можно раздавать сразу несколько подарков, поэтому в начале подарки будут отдаваться первому участнику, потом второму, и так далее. Известно, что если участнику достанется больше, чем \(t\) различных типов подарков, то участник будет слишком радоваться, и плохо напишет олимпиаду. Чтобы участники написали олимпиаду хорошо, было решено выдавать каждому участнику не более \(t\) различных типов подарков (при этом участнику может достаться несколько подарков одинакового типа).
Организаторы Закрытой олимпиады хотят сделать олимпиаду максимально эксклюзивной, и пригласить туда как можно меньше участников. Помогите организаторам узнать, какое минимальное число участников они могут позвать, чтобы все подарки были розданы участникам, а каждый получил не более \(t\) различных типов подарков.
Первая строка входных данных содержит три целых числа \(n\), \(k\) и \(t\) (\(1 \le n \le 300\,000\), \(1 \le k, t \le 10^9\)) — количество подарков в одной стопке, количество стопок с подарками и максимальное количество различных типов подарков, которое может достаться одному участнику.
Следующая строка содержит \(n\) целых чисел \(a_1,\ a_2,\ \ldots,\ a_n\) (\(1 \le a_i \le 10^9\)) — типы подарков, в порядке следования сверху вниз стопки.
Выведите единственное число — минимальное число участников, такое что все подарки будут им розданы, а каждый участник получит не более \(t\) различных типов подарков.
В первом примере стопка содержит следующие типы подарков (в порядке сверху вниз). Различными цветами обозначаются различные позиции в стопке.
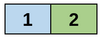

Так как \(t = 1\) каждый участник в данном случае может получить только подарки одного типа:

Во втором примере порядок выдачи подарков и итоговые комплекты подарков выглядят следующим образом:


В третьем примере порядок выдачи подарков следующий:

В данном случае одним из возможных оптимальных разбиений подарков на комплекты является следующее разбиение:

Тесты к этой задаче состоят из шести групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп.
| Доп. ограничения | ||||||
| Группа | Баллы | \(n\) | \(k\) | \(t\) | Необх. группы | Комментарий |
| 0 | 0 | – | – | – | – | Тесты из условия. |
| 1 | 14 | \(n \le 100\) | \(k \le 10\) | – | 0 | – |
| 2 | 12 | – | – | \(t = 1\) | – | – |
| 3 | 16 | \(n \le 1000\) | \(k \le 1000\) | – | 0, 1 | – |
| 4 | 21 | \(n \le 1500\) | \(k \le 10^6\) | – | 0, 1, 3 | – |
| 5 | 18 | – | \(k \le 10^6\) | – | 0, 1, 3, 4 | – |
| 6 | 19 | – | – | – | 0 – 5 | – |
2 4 1 1 2
8
4 3 1 1 1 2 1
7
7 2 3 1 2 3 4 5 6 7
5