Задача №115415. Поиск сокровищ
Для поиска полезных ископаемых ученые разработали специальный сканер.
Представим область для поисков как таблицу из \(k\) строк и \(n\) столбцов. Нумерация строк идет от \(1\) до \(k\) сверху вниз, нумерация столбцов от \(1\) до \(n\) слева направо. В каждой клетке таблицы могут находиться полезные ископаемые.
Сканер работает следующим образом: он может быть запущен в столбце \(p\) и возвращает количество клеток в зоне сканирования, которые содержат полезные ископаемые. Зона сканирования включает все клетки столбца \(p\), верхние \(k-1\) клетку столбца \(p-1\), верхние \(k-2\) клетки столбца \(p-2\), и так далее. На рисунке показана зона сканирования для поля с \(k = 3\), \(n=5\) и всех значений \(p\).
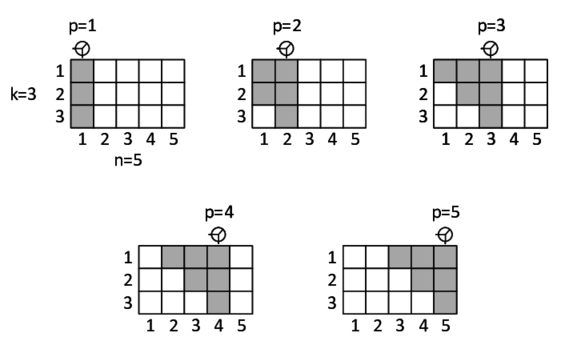
Вам даны значения, которые вернул сканер для всех \(p\), обозначим за \(b_p\) значение в столбце \(p\). Будем называть таблицу, где для каждой клетки определено, находятся ли в ней полезные ископаемые, корректной, если для нее сканер возвращает верные значения. Например, если в примере выше сканер вернул значения \([2, 1, 2, 3, 2]\), то одна из корректных таблиц может выглядеть следующим образом (клетки, содержащие ископаемые, обозначены черным треугольником):
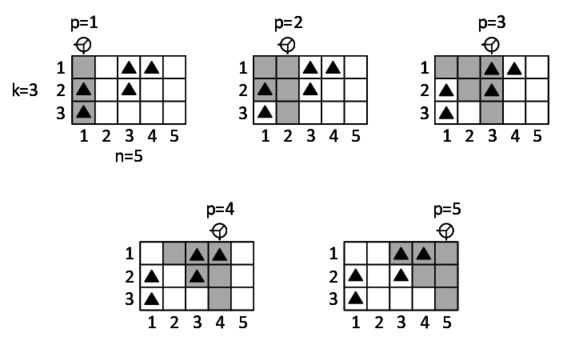
По заданным значениям, которые вернул сканер, определите количество корректных таблиц и выведите остаток от деления этого количества на число \(10^9+7\). Обратите внимание, что, возможно, сканер неисправен, и корректных таблиц вообще нет, тогда необходимо вывести \(0\).
В первой строке даны два числа \(n\), \(k\) — количество столбцов и строк, соответственно (\(1 \le n \le 200\), \(1 \le k \le 7\)).
Во второй строке даны \(n\) чисел \(b_1, b_2, \ldots, b_n\) — значения, которые вернул сканер (\(0 \le b_i \le k^2\)).
Выведите единственное число — остаток от деления количества различных корректных таблиц на \(10^9 + 7\).
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи и необходимых подзадач успешно пройдены.
| Подзадача | Баллы | Ограничения | Необходимые подзадачи | Информация о проверке |
| 1 | 7 | \(k \le 2\) | первая ошибка | |
| 2 | 9 | \(k \le 3\) | 1 | первая ошибка |
| 3 | 9 | \(k \le 4\) | 1, 2 | первая ошибка |
| 4 | 20 | \(k \le 5\) | 1–3 | первая ошибка |
| 5 | 15 | \(k \le 6\) | 1–4 | первая ошибка |
| 6 | 10 | \(1 \le n \cdot k \le 25\) | первая ошибка | |
| 7 | 30 | Без дополнительных ограничений | 1–6 | первая ошибка |
5 3 2 1 2 3 2
24