Задача №115444. Ленивые разрезы
Мальчику Антону нужно принести в школу на урок труда \(s\) клеточек. Антон очень ленивый, но очень любит уроки труда, поэтому сделать минимальное необходимое количество действий он готов.
Дома у Антона обнаружился клетчатый лист бумаги размера \(n \times m\), при этом \(s \le n \cdot m\). Также у Антона есть лазерный резак, который работает следующим образом:
- В резак устанавливается исходный лист бумаги
- Резак делает \(x\) прямых вертикальных разрезов по границам клеток
- Резак делает \(y\) прямых горизонтальных разрезов по границам клеток
- Из резака вынимается \((x + 1) \cdot (y + 1)\) новых клетчатых листов бумаги
Например, из листа \(3 \times 6\) за три разреза можно получить шесть листов с площадями \(4\), \(2\), \(6\), \(2\), \(1\) и \(3\).
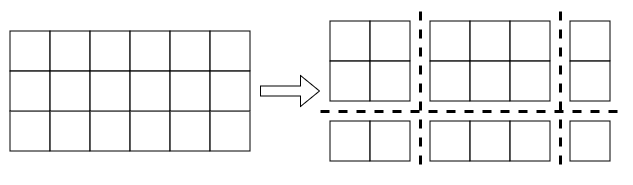
Так как Антон ленивый, он хочет сделать минимальное возможное число разрезов, чтобы из полученных из резака листов бумаги можно было собрать набор с суммой площадей ровно \(s\) клеток, который он принесет в школу на урок труда.
Антон боится перетрудиться в процессе работы с резаком, поэтому просит вас помочь определить минимальное возможное число разрезов, которые ему придется сделать.
В единственной строке даны три целых числа \(n\), \(m\) и \(s\) — размеры исходного клетчатого листа бумаги и необходимое для урока количество клеточек (\(1 \le n, m \le 10^5\), \(1 \le s \le n \cdot m\)).
Выведите одно целое число — минимальное возможное число разрезов, которые нужно сделать, чтобы из полученных листов бумаги можно было собрать набор с суммой площадей ровно \(s\) клеток.
На рисунке ниже представлены примеры разрезов для первых двух тестов из примера.
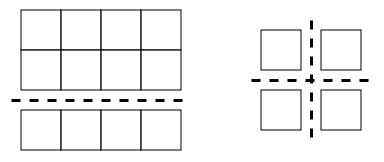
В третьем тесте из примера \(s = n \cdot m\), поэтому ничего резать не нужно.
3 4 8
1
2 2 3
2
10 9 90
0