Задача №115445. Декартов Кузнечик
Кузнечик по имени Декарт живет на Декартовой плоскости. Сегодня ему срочно нужно попасть из точки \((x_0, y_0)\) в точку \((x_1, y_1)\).
К сожалению, времени подумать у кузнечика нет, поэтому он строго решил прыгать \(n\) прыжков, при этом длина \(i\)-го прыжка должна быть в точности равна \(a_i\), ведь ему как раз приснилась именно такая последовательность чисел.
Помогите кузнечику составить маршрут из точки \((x_0, y_0)\) в точку \((x_1, y_1)\) с помощью прыжков длины \(a_i\), или подтвердите, что это невозможно.
В первой строке даны два целых числа \(x_0\) и \(y_0\) — координаты стартовой точки (\(-1000 \le x_0, y_0 \le 1000\)).
Во второй строке даны два целых числа \(x_1\) и \(y_1\) — координаты конечной точки (\(-1000 \le x_1, y_1 \le 1000\)). Обратите внимание, что стартовая и конечная точки маршрута кузнечика могут совпадать.
В третьей строке находится единственное целое число \(n\) — количество прыжков кузнечика (\(1\le n \le 10^5\)).
В четвертой строке заданы \(n\) целых чисел \(a_1, a_2 \dots a_n\) — желаемые длины прыжков (\(1\le a_i \le 1000\)).
Если допрыгать из стартовой точки в конечную данной последовательностью прыжков невозможно, выведите в первой строке « Impossible ».
Иначе, в первой строке выведите « Possible », а в следующих \(n\) строках выведите координаты точек. В \(i\)-й строке должны быть выведены два вещественных числа — координаты точки, в которой кузнечик окажется после \(i\)-го прыжка.
Если существует несколько решений, разрешается вывести любое. При этом следующие величины должны быть равны с относительной или абсолютной погрешностью не более \(10^{-4}\):
- Расстояние между \((i-1)\)-й и \(i\)-й точками в ответе должно быть равно \(a_i\);
- Расстояние между стартовой и первой в ответе точками должно быть равно \(a_1\);
- Координаты \(n\)-й точки в ответе должны быть равны координатам конечной точки.
Один из возможных маршрутов кузнечика для первого теста из примера представлен на рисунке.
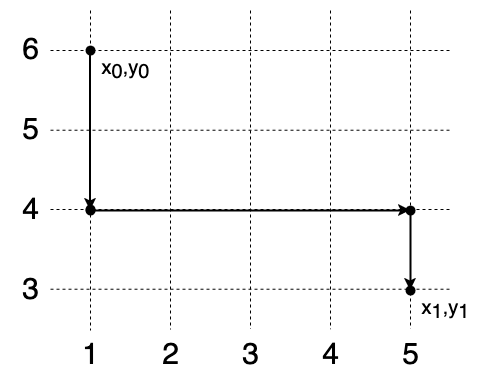
1 6 5 3 3 2 4 1
Possible 0.14424492 4.19232656 4.02884898 3.23846531 5.00000000 3.00000000
0 0 6 8 5 2 3 4 5 6
Possible -1.20000000 -1.60000000 -3.00000000 -4.00000000 -0.60000000 -0.80000000 2.40000000 3.20000000 6.00000000 8.00000000
-10 10 10 -10 2 5 5
Impossible