Задача №115452. Мультимино
Назовём \(n\)-миношкой связную фигуру, составленную из \(n\) квадратиков \(1 \times 1\). Скажем, что две \(n\)-миношки совпадают, если одну из них можно перевести в другую, используя операции сдвига, поворота и отражения.
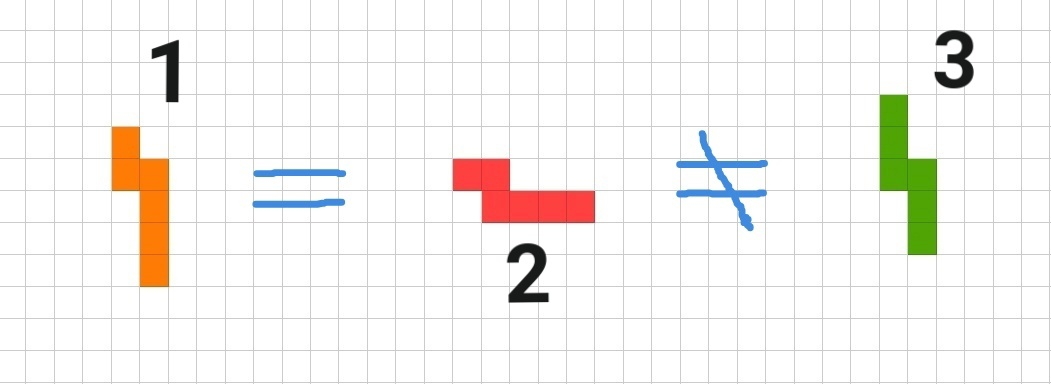
Например, на рисунке снизу красная гексаминошка (номер \(2\)) совпадает с оранжевой (номер \(1\)), и они обе не равны зелёной (номер \(3\)).
По данному вам числу \(n\) разрежьте клетчатое поле размера \(n \times n\) квадратиков на \(n\) попарно различных непересекающихся \(n\)-миношек или сообщите, что такого разрезания не существует.
В единственной строке входных данных находится целое число \(n\) (\(1 \leqslant n \leqslant 100\)).
Выведите единственное число \(-1\), если нужного разбиения не существует.
Иначе пронумеруем \(n\)-миношки натуральными числами от \(1\) до \(n\). Выведите \(n\) строк по \(n\) чисел в каждой, соответствующие разбиению поля на \(n\)-миношки по принципу, что клетка в \(i\)-ом столбце и \(j\)-ой строке принадлежит \(n\)-миношке номер \(a_{ij}\) (\(1 \leqslant a_{ij} \leqslant n\)).
Все \(n\)-миношки в разбиении должны быть связны и попарно различны между собой. Если для поля существует несколько корректных разбиений, выведите любое из них.
В первом примере разбиение выглядит как на рисунке слева.
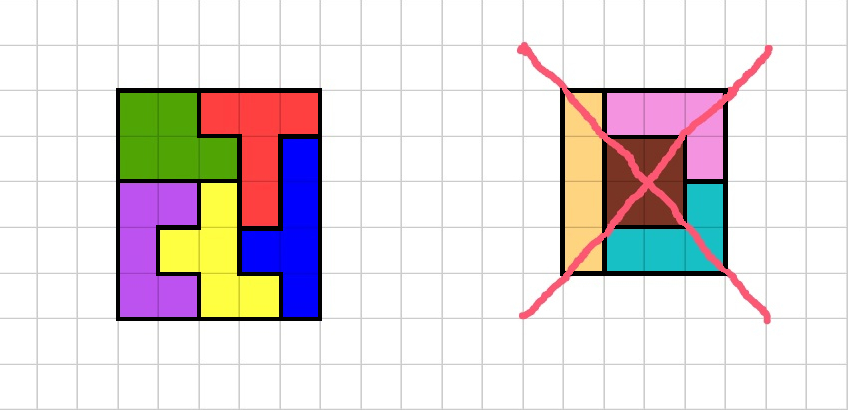
Во втором примере рисунок справа не будет корректным разбиением, так как сиреневая (верхняя) и бирюзовая (нижняя) \(n\)-миношки могут быть переведены друг в друга сдвигом, поворотом и симметрией, а следовательно, равны.
5
4 4 2 2 2 4 4 4 2 3 5 5 1 2 3 5 1 1 3 3 5 5 1 1 3
4
-1