Задача №2919. Борьба с пробками
Город Нью-Йорк практически парализован гигантским количеством пробок. Мэр Джулио Джулиани предложил новую схему движения по городским улицам. Все улицы по этому плану должны стать односторонними.
Город расположен на прямоугольном острове размером M на N квадратных футов. (M футов с юга на север и N футов с запада на восток. Город разделен на кварталы улицами, идущими с запада на восток и авеню, идущими с юга на север. Длина каждого из кварталов составляет 200 футов (строго говоря, это расстояние между двумя параллельными улицами, окружающими квартал). Улицы нумеруются с юга на север начиная с единицы. Авеню нумеруются с запада на восток также с единицы.
Одностороннее движение организовано так, как показано на рисунке.
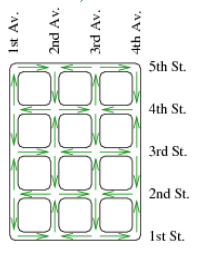
Мэр хочет проехать от одного перекрестка до другого. Определите минимальное расстояние между этими перекрестками. Для простоты можно игнорировать расстояние пройденное на перекрестках, т.е. расстояние пройденное вдоль квартала составляет ровно 200 футов.
Входной файл состоит из 4 строк
Первая строка содержит число M (400 ≤ M ≤ 1000000). Следующая строка содержит число N (400 ≤ N ≤ 1000000). Оба числа делятся на длину квартала. Следующие две строки описывают начальный и конечный перекресток. Каждое описание перекрестка задается так:
m Av., n St.
Например,
1st Av., 5th St.
Выведите минимальное расстояние между перекрестками.
800 600 1st Av., 1st St. 2nd Av., 3rd St.
1000