Задача №498. Кубики
Родители подарили мальчику Пете очень много одинаковых кубиков. Наиболее интересным сооружением из кубиков Петя счел двусторонние лесенки.
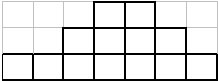
В основании (нижнем ряду) такой лесенки расположено \(N\) кубиков, а каждый следующий ряд кубиков укладывается на предыдущий так, что один кубик укладывается ровно на один нижестоящий кубик, а по крайней мере на самый правый и самый левый кубики предыдущего ряда новые кубики не кладутся (чтобы получилась ступенька).
Петя поручил старшему брату подсчитать, сколько можно построить различных лесенок, состоящих из ровно \(K\) рядов кубиков, в основании которых лежит ровно \(N\) кубиков. При этом, если одну лесенку можно получить из другой путем зеркального отображения, то они все равно считаются различными.
Вводятся два числа \(N\) и \(K\) (\(1 \le N \le 100\), \(1 \le K \le 100\)).
Выведите одно число – количество различных лесенок. Гарантируется, что правильный ответ не будет превышать \(10^{18}\).
10 4
84