Задача №961. Фен шуй
Фен шуй – это древняя китайская практика размещения предметов в пространстве для достижения гармонии. В ней говорится, что пол не должен быть пустым, поэтому Фил разместил на полу два одинаковых круглых ковра (по фен шуй надо избегать прямых линий и острых углов).
К сожалению, ими нельзя покрыть пол комнаты полностью, так как она имеет форму выпуклого многоугольника. Фил хочет минимизировать непокрытую часть пола, располагая ковры оптимальным образом.
Помогите ему расположить два ковра в комнате так, чтобы общая покрытая площадь была максимальна. Ковры можно накладывать друг на друга, но их нельзя загибать и резать.
Первая строка входных данных содержит два целых числа \(n\) и \(r\) — число углов в комнате \((3 \le n \le 100)\) и радиус ковров (\(1 \le r \le 1000\), оба ковра имею один и тот же радиус). Следующие n строк содержат по два числа \(x_i\) и \(y_i\) — координаты \(i\)-го угла \((–1000 \le x_i; y_i \le 1000). Углы описаны в порядке обхода комнаты по часовой стрелке. Координаты углов различны и соседние стены не коллинеарны.
Выведите \)x_1, y_1, x_2, y_2\(, где \)(x_1, y_1)\( и \)(x_2, y_2)$ обозначаю центры ковров. Координаты должны иметь точность не менее 4 цифр после точки. Выведите любое оптимальное расположение. Входные данные гарантируют, что решение существует (Фил не стал бы покупать ковер, который не помещается в комнату).
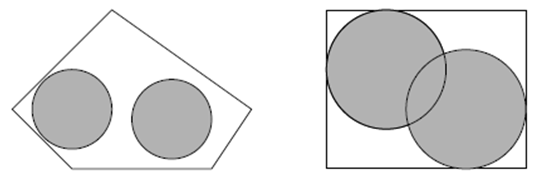
5 2 -2 0 -5 3 0 8 7 3 5 0
-2.1715728753 3.0000000000 4.2617090669 2.4981148759
4 3 0 0 0 8 10 8 10 0
3.0000000000 5.0000000000 7.0000000000 3.0000000000