Задача №963. Японский кроссворд
Наиболее известная игра, дошедшая до нас из Японии – это Судоку. Новая игра должна затмить ее славу. Про нее известно следующее. Нам дан квадрат, разделенный сеткой на n×n клеток, а каждая клетка содержит картинку одного из k типов. Игрок должен переместить их, чтобы получить максимально возможное число одинаковых первых рядов (два ряда считаются одинаковыми, если оба заполнены одинаковыми картинками и в одинаковом порядке). По виду таблицы определите, сколько одинаковых рядов в ней можно сложить (если менять картинки как угодно).
Например, если нам дана такая таблица:
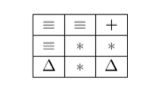
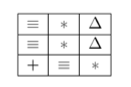
одно из результирующих состояний в игре будет
Первая строка входных данных содержит два числа n (\(1\leq n \leq 40000\)) и k (\(1 \leq k \leq 50000\)). Каждая из следующих k строк содержит число картинок в таблице каждого из k типов. Все числа больше 0, их сумма в точности равна \(n^2\).
Выведите в первой строке максимальное количество одинаковых рядов, которые можно построить из этих картинок. В следующих n строках выведите содержание таких рядов: в каждой строке должно находиться одно число – номер соответствующей картинке в порядке ее появления во входных данных. Если решений несколько, выведите любое из них.
3 4 3 3 2 1
2 1 2 3