Задача №115214. Посадка в самолет
В самолетах авиакомпании Битавиа кресла расположены в \(n\) рядов, при этом в каждом ряду по шесть мест, между третьим и четвертым местом находится проход. Некоторые пассажиры регистрируются заранее онлайн, другие пассажиры регистрируются на стойке регистрации в аэропорту.
При онлайн-регистрации пассажир может выбрать любое место и не может его затем менять. Например, при \(n = 6\) рассадка в самолете после онлайн-регистрации может выглядеть так (крестиками отмечены занятые места):
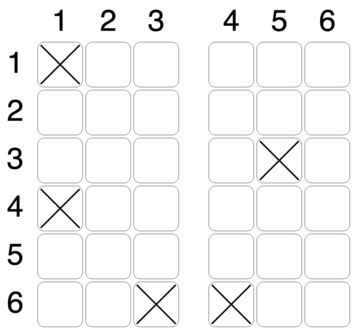
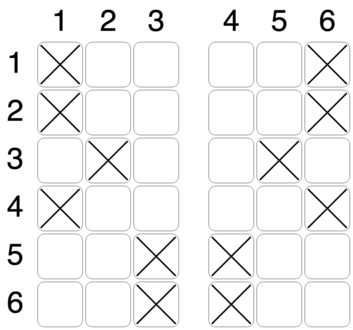
На стойку регистрации придут \(m\) пассажиров. По правилам Битавиа нужно рассадить их в самолете таким образом, чтобы итоговая рассадка в самолете была симметрична относительно прохода. То есть, если в некотором ряду на первом кресле сидит пассажир, то в том же ряду на шестом кресле тоже должен сидеть пассажир. То же самое справедливо для второго и пятого, третьего и четвертого кресел, соответственно. При этом пересаживать пассажиров, прошедших онлайн-регистрацию нельзя. В исходную рассадку, показанную на рисунке выше, можно добавить семь пассажиров, удовлетворив условие симметрии, например, следующим образом:
Вам дана рассадка пассажиров после онлайн-регистрации. Требуется рассадить \(m\) пассажиров так, чтобы итоговая рассадка в самолете была симметрична относительно прохода, или определить, что это невозможно.
В первой строке содержатся два целых числа \(n\) и \(m\) — количество рядов в самолете и количество пассажиров, которые придут на стойку регистрации (\(1 \le n \le 1000\), \(0 \le m \le 6000\)).
В следующих \(n\) строках задана изначальная рассадка в самолете после онлайн-регистрации. В каждой строке содержится по шесть символов, при этом \(i\)-й символ \(j\)-й строки равен « X » (заглавная английская X), если \(i\)-е место в \(j\)-м ряду уже занято и « . » (точка) иначе.
Если искомой рассадки не существует, выведите « Impossible ».
Иначе выведите \(n\) строк по шесть символов — итоговую рассадку в самолете. При этом \(i\)-й символ \(j\)-й строки должен быть равен « X », если место занято, и « . », если свободно. Если существует несколько решений, разрешается вывести любое.
Баллы за каждую подзадачу начисляются только в случае, если все тесты для этой подзадачи и необходимых подзадач успешно пройдены.
| Подзадача | Баллы | Дополнительные ограничения | Необходимые подзадачи | Информация о проверке |
| 1 | 15 | \(m = 0\) | первая ошибка | |
| 2 | 16 | Изначально в самолете все места свободны | первая ошибка | |
| 3 | 17 | \(m = 1\) | первая ошибка | |
| 4 | 18 | Изначально в самолете занято ровно одно место | первая ошибка | |
| 5 | 34 | нет | 1–4 | первая ошибка |
Выше приведены пять примеров входных данных.
-
В первом примере \(m = 0\), а рассадка в самолете симметрична, поэтому итоговая рассадка совпадает с исходной.
-
Во втором примере есть только один способ рассадить пассажиров симметрично.
-
В третьем примере существовало бы решение, при \(m = 1\), но при \(m = 2\) не существует способа рассадить всех пассажиров симметрично.
-
В четвертом примере требуется рассадить больше пассажиров чем свободных мест в самолете.
-
Пятый примере соответствует ситуации, рассмотренной на рисунках в тексте условия. В этом примере существует несколько решений, приведено одно из них.
1 0 X.XX.X
X.XX.X
2 1 X.XX.X ..X...
X.XX.X ..XX..
3 2 X.XX.X ...... X..X.X
Impossible
1 103 .X.XXX
Impossible
6 7 X..... ...... ....X. X..... ...... ..XX..
XXXXXX ...... .X..X. X....X ...... ..XX..