Задача №115375. Хоровод
Есть группа из \(x\) мальчиков и \(y\) девочек. Рассмотрим хоровод, составленный из них, в котором дети пронумерованы от \(1\) до \(x + y\) по часовой стрелке.
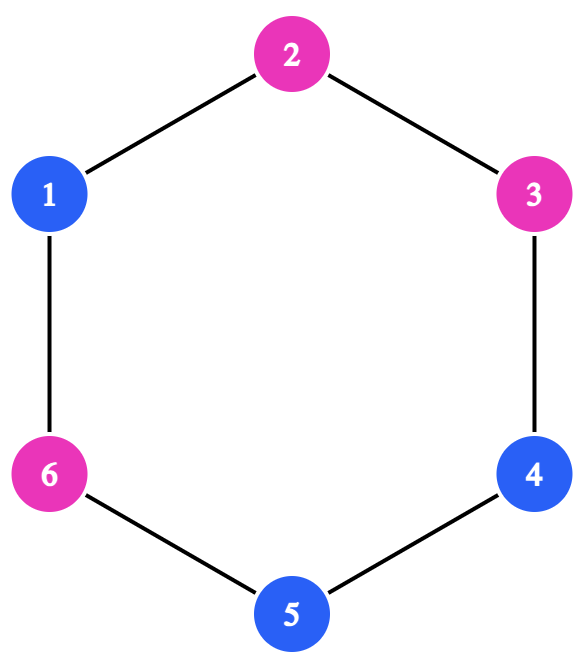
На рисунке выше изображён хоровод из трёх мальчиков (номера \(1\), \(4\) и \(5\)) и трёх девочек (номера \(2\), \(3\) и \(6\)). Этот хоровод можно описать строкой BGGBBG , где \(i\)-й символ обозначает пол человека на \(i\)-й позиции в хороводе. Символ B обозначает мальчика, символ G обозначает девочку.
Определите, можно ли составить хоровод из всех мальчиков и девочек в группе, в котором есть ровно \(m\) пар соседей разного пола. Например, на рисунке выше есть \(4\) такие пары: \((1, 2)\), \((3, 4)\), \((5, 6)\) и \((6, 1)\).
Первая строка содержит одно целое число \(x\) (\(2 \le x \le 100\)) — количество мальчиков в хороводе.
Вторая строка содержит одно целое число \(y\) (\(2 \le y \le 100\)) — количество девочек в хороводе.
Третья строка содержит одно целое число \(m\) (\(2 \le m \le 200\)) — необходимое количество пар соседей разного пола.
В первой строке выведите « YES » (без кавычек), если мальчиков и девочек можно расставить в хороводе требуемым образом, и « NO » (без кавычек) иначе.
Если требуемая расстановка существует, во второй строке выведите строку длины \(x + y\), содержащую \(x\) символов B (мальчик) и \(y\) символов G (девочка). Эта строка должна описывать любой хоровод, в котором есть ровно \(m\) пар соседей разного пола. Обратите внимание, что первый и последний символ строки описывают соседних детей в хороводе.
В данной задаче \(20\) тестов, помимо тестов из условия, каждый из них оценивается в \(5\) баллов. Результаты работы ваших решений на всех тестах будут доступны сразу во время соревнования.
Решения, корректно работающие при \(x = y\), наберут не менее \(30\) баллов.
Хоровод из первого примера изображён в условии задачи.
Во втором примере не существует хоровода из \(2\) мальчиков и \(2\) девочек, в котором есть ровно \(3\) пары соседей разного пола.
В третьем примере есть ровно \(4\) пары соседей разного пола: \((1, 2)\), \((2, 3)\), \((3, 4)\), \((4, 5)\).
3 3 4
YES BBGBGG
2 2 3
NO
3 2 4
YES GBGBB
2 2 100
NO