Открытая олимпиада школьников по программированию

Задача №115408. Сильная связность наносит ответный удар

Вершины $u$ и $v$ ориентированного графа называются сильно связными, если в графе существует путь из $u$ в $v$ и путь из $v$ в $u$. Заметим, что если $u$ и $v$, а также $v$ и $w$ сильно связны, то $u$ и $w$ сильно связны. Поэтому вершины графа разбиваются на множества — компоненты сильной связности. Вершина, принадлежащая компоненте сильной связности, сильно связна со всеми вершинами компоненты (в том числе с собой) и не сильно связна со всеми остальными вершинами.

На занятии по графам Алиса нарисовала на доске ориентированный граф на $n$ вершинах, а также выделила его компоненты сильной связности. Во время перерыва Боб решил разыграть Алису и стереть направления на некоторых рёбрах графа. При этом он хочет, чтобы после перерыва Алиса смогла однозначно восстановить стёртые направления по остальным рёбрам и разбиению на компоненты сильной связности.

Помогите Бобу, сообщив, на каком максимальном количестве рёбер графа он может стереть направления, а также скольким количеством способов он может это сделать.

Более формально, найдите максимальный размер подмножества рёбер графа $A$, обладающего следующим свойством: если стереть направления рёбер в множестве $A$, то на основе информации о старых компонентах сильной связности и направлениях рёбер не из множества $A$ можно единственным образом восстановить направления рёбер из множества $A$ так, чтобы компоненты сильной связности остались прежними.

Поскольку количество таких максимальных подмножеств может быть очень большим, выведите его по модулю $10^9 + 7$.

Решения, корректно определяющие максимальный размер множества $A$, но неправильно предъявляющие количество таких множеств, будут получать частичные баллы.

Входные данные

Первая строка содержит три целых числа $n$, $m$ и $g$ ($2 \le n \le 2000$, $1 \le m \le 2000$, $0 \le g \le 7$) — количество вершин и рёбер графа соответственно, а также номер группы тестов.

Следующие $m$ строк содержат по два целых числа $u_i$ и $v_i$ ($1 \le u_i, v_i \le n$, $u_i \neq v_i$) — номера вершин, являющихся началом и концом $i$-го ребра.

Гарантируется, что для любых $1 \le i, j \le n$ $(u_i, v_i) \neq (u_j, v_j)$ и $(u_i, v_i) \neq (v_j, u_j)$, то есть любые две вершины соединены не более чем одним ребром, вне зависимости от направления.

Выходные данные

В первой строке выведите единственное число — размер максимального подмножества рёбер, на котором можно стереть направления.

Во второй строке выведите единственное число — количество таких подмножеств по модулю $10^9 + 7$. Если вы не хотите предъявлять количество таких подмножеств, то во второй строке, вместо этого, выведите любое число от $-1$ до $10^9 + 6$. В этом случае ваше решение получит часть баллов за тест.

Обратите внимание, что отсутствие какого либо числа во второй строке приводит к вердикту «Неправильный ответ» и нулю баллов за этот тест, несмотря на правильность размера подмножества.

Примечание

Граф из примера с выделенными компонентами сильной связности:

$\text{[math]}$

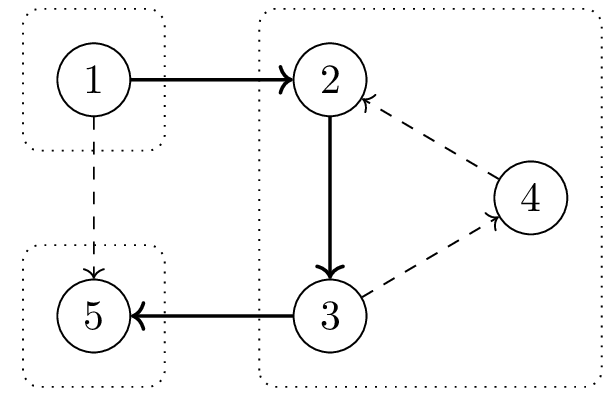
На рёбрах, выделенных пунктиром, можно стереть направления. Действительно, ребро $(1, 5)$ не может быть ориентировано в другую сторону, потому что иначе вершины $1$, $2$, $3$ и $5$ будут лежать в одной компоненте сильной связности. Рёбра $(3, 4)$ и $(4, 2)$ не могут быть ориентированы иначе, потому что тогда вершины $2$, $3$ и $4$ не будут лежать в одной компоненте сильной связности.

Рассмотрим некорректный способ выбрать подмножество рёбер:

$\text{[math]}$

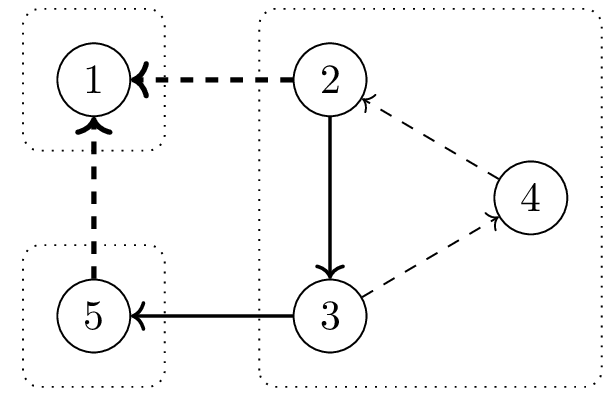
Здесь нельзя стереть направления на рёбрах, выделенных жирным пунктиром. Например, если ориентировать рёбра $(1, 2)$ и $(1, 5)$ в другую сторону, получится граф с таким же разбиением на компоненты сильной связности.

Можно показать, что нельзя стереть направления на $4$ рёбрах, поэтому ответ — $3$.

Система оценки

Тесты к этой задаче состоят из семи групп. Правила, по которым выставляются баллы за подгруппы описаны ниже. Обратите внимание, что прохождение тестов из условия не требуется для некоторых групп.

Если во всех тестах группы правильно посчитан размер максимального подмножества рёбер, на котором можно стереть направления и количество таких подмножеств, за группу выставляется полный балл.

В противном случае, если во всех тестах группы правильно посчитан размер максимального подмножества рёбер, на котором можно стереть направления, а количество оказалось неверным хотя-бы в одном тесте группы, за группу выставляется частичный балл. Обратите внимание, что группы, зависящие от неё, в таком случае будут запущены для тестирования и даже могут быть оценены в полный балл.

	Баллы		Доп. ограничения
Группа	Частичные	Полные	$n$	$m$	Необх. группы	Комментарий
0	0	0	–	–	–	Тесты из условия.
1	7	11	$n \le 14$	$m \le 14$	0
2	5	9	$n \le 20$	$m \le 20$	0, 1
3	8	12	–	–	–	$u_i \lt v_i$, для всех $1 \le i \le n - 1$ есть ребро $(i, i + 1)$
4	8	13	–	–	3	$u_i \lt v_i$
5	12	20	–	–	–	для всех $1 \leqslant i \leqslant n - 1$ есть ребро $(i, i + 1)$, есть ребро $(n, 1)$
6	13	21	–	–	5	граф состоит из одной компоненты сильной связности
7	8	14	–	–	0 – 6

Примеры

Входные данные

Выходные данные

3
3

Сдать: для сдачи задач необходимо войти в систему