Задача №3366. Дятлы
В парке растут два очень высоких дерева, на стволе каждого из которых расположены дупла одно под другим на равном расстоянии друг от друга. Однажды N дятлов решили заселить эти дупла. Некоторые из них знакомы и поэтому хотели бы иметь возможность летать друг к другу в гости. Дятлы летают прямолинейно и очень быстро. Чтобы уменьшить вероятность столкновения, они решили селиться по следующему принципу:
Каждые две дятла, которые хотят летать друг к другу в гости, должны жить на разных деревьях Отрезки, соединяющие дупла знакомых между собой дятлов не пересекаются (однако их концы могут совпадать).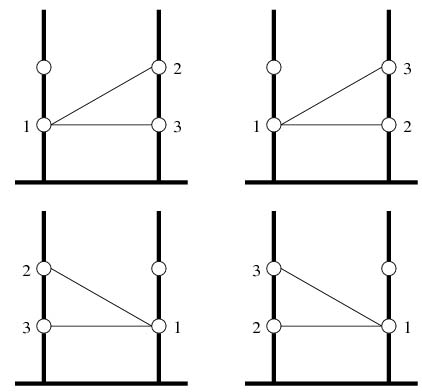
Кроме того, дятлы хотят жить как можно ниже, т.е. на каждом из деревьев они занимают дупла подряд, начина снизу. На каждом из деревьев больше дупел, чем общее количество дятлов.Как известно, у дятлов очень маленький мозг. Поэтому вам следует подумать за них и сообщить, сколькими способами они могут разместиться в дуплах. Т.к. дятлы также плохо воспринимают большие числа, ответ следует вывести по модулю K.
В первой строке содержатся три числа: \(N\) – количество дятлов (\(1 \leq N \leq 10^6\)), \(M\) – количество пар знакомых дятлов (\(1 \leq M \leq 10^7\)) и число \(K\) (\(1 \leq K \leq 2\times 10^6\)). Дятлы занумерованы от \(1\) до \(N\). В следующих \(M\) строках заданы два числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq N\)), задающие пару знакомых дятлов.
Вывод должен содержать одно число: количество вариантов размещения по модулю K.
3 2 10 1 2 1 3
4
4 4 17 1 2 1 3 4 2 3 4
0