ЛОШ-2016: А ты купи остов

Большое количество соревнований по разным видам спорта проводится по так называемой "олимпийской системе". В простейшем варианте она состоит в следующем. В турнире участвуют N = 2^k игроков. Они получают номера от 1 до N, и в первом круге игрок 1 играет с игроком 2, игрок 3 с игроком 4 и т. д., игрок (N - 1) — с игроком N. Проигравшие в каждой паре выбывают из соревнований, а победители проходят во второй круг. Там победитель первой пары (т. е. игрок 1 или игрок 2) играет с победителем второй пары и т. д. Таким образом, в первом круге участвуют N = 2^k игроков, во втором круге — 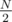= 2^k - 1 и т. д., в финале участвуют два игрока.

Серьезной проблемой является то, что некоторые сильные игроки могут встретиться между собой уже в одном из первых кругов, в результате чего некоторые сильные участники могут рано выбыть из борьбы, в то время как другие, менее сильные участники, могут пройти намного выше, если им повезет с соперниками. Для борьбы с этим эффектом применяется так называемый “рассев” игроков, когда начальная нумерация участников не является полностью случайной, и вероятность “везения”/”невезения” с соперниками резко уменьшается.

В этой задаче вам нужно будет написать программу, находящую в некотором смысле оптимальный “рассев” игроков. Для этого рассмотрим следующую модель. Предположим, что участников можно упорядочить по силе так, что более сильный игрок всегда будет выигрывать у более слабого. В таком случае по изначальному “рассеву” игроков дальнейший ход соревнований будет однозначно определен. Тогда в качестве критерия оптимальности рассева” можно потребовать выполнение следующих условий: в финале играют двое сильнейших игроков, в полуфиналах играют четверо сильнейших игроков, и т. д.: в каждом круге играют только сильнейшие игроки (т. е. если в каком-то круге m мест, то в этом круге должны участвовать m сильнейших игроков). Вам дано N. Найдите любой оптимальный рассев N игроков.