Задача №113915. Расшифровка
Известно, что если сохранить в каждом слове текста первую и последнюю букву, а остальные переставить произвольным образом, получившийся текст по-прежнему можно достаточно свободно прочитать. В лаборатории информатики исследуют аналогичный феномен для числовых последовательностей.
Будем называть последовательность, состоящую из целых положительных чисел, корректной , если первое число в этой последовательности является минимальным, а последнее — максимальным. Например, последовательности [1, 3, 2, 4] и [1, 2, 1, 2] являются корректными, а последовательность [1, 3, 2] — нет.
Задана последовательность [ a 1 , a 2 , ..., a n ] . Будем называть отрезок элементов заданной последовательности [ a l , a l + 1 , ..., a r ] корректным, если он представляет собой корректную последовательность: a l является минимальным числом на этом отрезке, а a r — максимальным.
В рамках исследования необходимо разбить заданную последовательность на минимальное количество непересекающихся корректных отрезков. Например, последовательность [2, 3, 1, 1, 5, 1] можно разбить на три корректных отрезка: [2, 3] и [1, 1, 5] и [1] .
Требуется написать программу, которая по заданной последовательности определяет, на какое минимальное количество корректных отрезков её можно разбить.
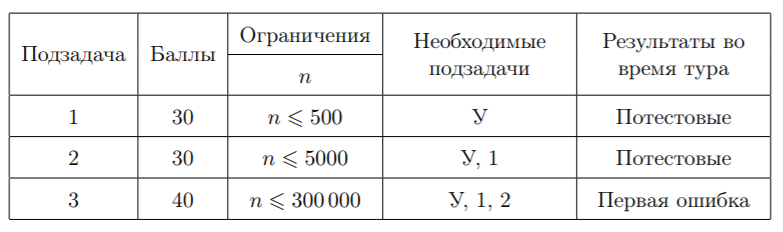
Первая строка входных данных содержит целое число n ( 1 ≤ n ≤ 300 000 ) — количество элементов в заданной последовательности.
Вторая строка содержит n целых чисел a 1 , a 2 , ..., a n — заданную последовательность ( 1 ≤ a i ≤ 10 9 ).
Выведите одно число — минимальное количество корректных отрезков, на которое можно разбить заданную последовательность.
5 5 4 3 2 1
5
4 1 3 2 4
1
6 2 3 1 1 5 1
3