Задача №1717. Подсветка зданий
Харбин знаменит своей ночной подсветкой зданий. К сожалению, экономический кризис не обошел стороной и этот город. Аудит показал, что освещение улиц - самая большая статья городского бюджета. Соответственно, было принято решение удешевить подсветку, но так, чтобы это не повлияло на ее качество, ибо мэр не хотел, чтобы пострадала репутация города среди туристов.
Рассмотрим двумерную модель города, где каждое здание описывается тремя числами \(L\), \(R\), \(H\) и имеет вид прямоугольника со сторонами, параллельными осям координат, противоположные углы которого имеют координаты (\(L\), 0) and (\(R\), \(H\)). Прямоугольники не пересекаются и даже не касаются. Мэр планирует осветить город несколькими фонарями, расположенными на крышах зданий (возможно, на углах крыш). На одном здании может быть произвольное количество фонарей. Известно, что фонарь, расположенный в точке (\(x_1\), \(y_1\)) освещает все точки (\(x_2\), \(y_2\)) такие что соединяющий их отрезок не содержит внутренних точек ни одного из зданий (но может содержать любое, в том числе и бесконечное количество точек границ зданий и углов).
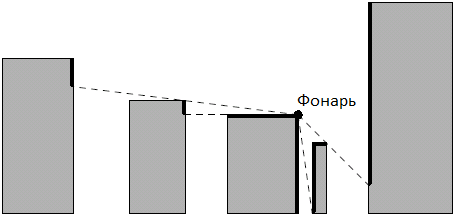
На рисунке выше показан фонарь и все освещаемые им точки на границах зданий
Требуется расположить минимальное количество фонарей так, чтобы осветить все боковые стороны зданий. Сторона считается освещенной, если каждая ее точка (включая концы) освещена хотя бы одним источником.
Входные данные содержат несколько тестовых примеров. Первая строка содержит число \(T\) (1 \(\le\) \(T\) \(\le\) 10000) - количество тестовых примеров. Далее следует \(T\) блоков, содержащих тестовые примеры.
Первая строка каждого блока содержит натуральное число \(N\) (1 ≤ \(N\) ≤ 1000) - количество зданий в городе. Каждая из следующих \(N\) строк содержит три числа \(L\), \(R\) и \(H\) (1 \(\le\) \(L\) < \(R\) 10000, 1 \(\le\) \(H\) \(\le\) 10000), описывающие одно из зданий.
Сумма квадратов значений \(N\) по всем тестовым примерам во входных данных не превосходит 1 000 000.
Для каждого тестового примера выведите в отдельной строке одно натуральное число - минимальное количество фонарей.
Потестовая оценка.
2 4 3 4 1 5 6 1 7 8 1 1 2 10 6 3 4 1 5 6 1 7 8 1 1 2 10 11 12 10 9 10 1
5 4