РОлЗ: Problems

Два неориентированных графа G и H называются изоморфными , если:

• они имеют одинаковое количество вершин;
• существует такое однозначное соответствие между их вершинами, что любые две различные вершины графа G соединены ребром тогда и только тогда, когда соединены ребром соответствующие вершины графа H.

Например, следующие два графа изоморфны, хотя выглядят по-разному:

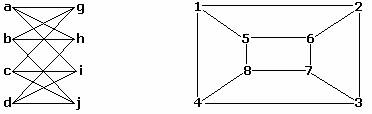
Возможным однозначным соответствием, показывающим, что эти два графа изоморфны, является {a-1, b-6, c-8, d-3, g-5, h-2, i-4, j-7}, хотя существуют и другие подобные соответствия.

Подграфом графа G называется граф, множества вершин и ребер которого являются подмножествами множеств вершин и ребер графа G. Заметьте, что граф G является также и своим подграфом. На рисунке показаны граф и один из его подграфов:

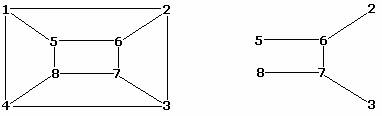
Говорят, что граф G содержит другой граф H , если существует хотя бы один подграф H ’ графа G , который изоморфен H . Следующий рисунок показывает граф G , который содержит граф H .

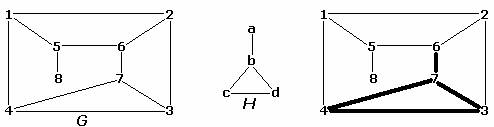
ЗАДАНИЕ

По двум заданным неориентированным графам G и H постройте подграф G’ графа G такой, что:

• количество вершин в графах G и G’ одинаково;
• H не содержится в G’ .

Естественно, может быть много подграфов графа G’ с перечисленными свойствами. Постройте подграф с как можно большим количеством ребер.

БАЗОВЫЙ АЛГОРИТМ

Возможно, наиболее простой стратегией при решении этой задачи будет следующая: рассматривать ребра графа G в порядке, в котором они представлены во входных данных, после чего пытаться добавлять ребра одно за другим в граф G’, проверяя на каждом шаге, входит ли граф H в граф G’ или нет. Правильная реализация этого жадного алгоритма наберет некоторое количество очков, хотя существуют гораздо лучшие стратегии.

ОГРАНИЧЕНИЯ

ВВОД

Вы получите 10 файлов с именами от forbidden1.in до forbidden10.in, каждый со следующими данными:

Заметьте, что за исключением строки 1, приведенные входные данные представляют собой матрицы смежности графов H и G .

ВЫВОД

Вы должны создать 10 файлов по одному на каждый входной. Каждый файл должен содержать следующие данные:

Заметьте, что за исключением строк 1 и 2, приведенные входные данные представляют собой матрицу смежности графа G’. Обратите внимание, что есть много вариантов ответа, и приведенный вариант является корректным, но не оптимальным.

ОЦЕНИВАНИЕ
Ваши баллы будут зависеть от количества ребер в графе G’, который Вы получите. Количество баллов определяется следующим образом: Вы получите ненулевое количество баллов для каждого выходного файла, только если он соответствует условиям задачи. В этом случае количество баллов вычисляется так: пусть E_y будет количеством ребер в Вашем ответе, E_b  – количество ребер графа G’, которое вычислено БАЗОВЫМ АЛГОРИТМОМ, E_m  – максимальное количество ребер в выводах всех участников. Количество полученных баллов определяется следующим образом:

• 30 E_y / E_b    – если E_y ≤ E_b,
• 30 + 70(E_y - E_b)/ (E_m - E_b)  – если E_y > E_b.