Задача №1053. Pinball
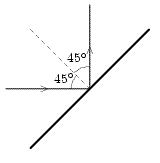
Поле в Pinball представляет собой прямоугольник без стенок, состоящий из n x m квадратных клеток, (n клеток по вертикали, m клеток по горизонтали). Клетки по вертикали нумеруются сверху вниз, по горизонтали - слева направо. В каждой клетке можно установить одну отражающую пластинку в одном из двух положений: в положении 1 - от левого верхнего угла к правому нижнему или в положении 2 - от левого нижнего к правому верхнему. Летящий шарик при столкновении с пластинкой изменяет свою траекторию, при этом угол падения шарика всегда равен углу отражения и составляет 45° (см. рисунок).
На границе прямоугольника заданы две точки A и B, являющиеся серединами сторон некоторых клеток поля. Пластинки расставляются таким образом, чтобы шарик, запущенный из точки A, попал в точку B. При этом шарик начинает движение внутрь поля перпендикулярно стороне клетки, на которой находится точка A.
| | 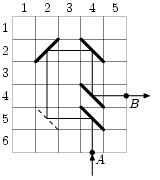 |
Изначально на поле были расставлены k пластинок таким образом, чтобы шарик попал из точки A в точку B. После этого одну из пластинок удалили. Необходимо определить, куда и как можно поставить удаленную пластинку, чтобы шарик, выпущенный из точки A, попал в точку B. При этом требуется, чтобы длина пути шарика была минимальной. Пластинку нужно поставить на некоторую свободную клетку даже в том случае, если шарик попадает в точку B и без нее.
Требуется написать программу, устанавливающую пластинку таким образом, чтобы шарик попадал из точки A в точку B и длина его пути была минимальна.
Первая строка входного файла содержит три числа: n, m (1 ≤ n, m ≤ 1000) и k, где k - общее количество пластинок, которые были исходно расставлены.
Во второй строке указываются номера клетки по вертикали и по горизонтали, на границе которой лежит точка A, и номер стороны,на которой она находится. Стороны клетки пронумерованы целыми числами от 1 до 4, при этом верхней стороне присвоен номер 1, далее по часовой стрелке нумеруются остальные стороны.
Третья строка содержит описание точки B в том же формате.
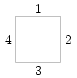 | 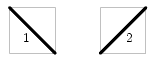 |
| Номера сторон клеток | Возможные положения пластинок |
Следующие k-1 строк описывают пластинки, оставшиеся на поле. В каждой строке записаны по три числа: первое - номер клетки по вертикали, второе - номер клетки по горизонтали, третье - положение пластинки в клетке (число 1 или 2).
Выходной файл должен содержать три числа: номера клетки, в которую следует поставить пластинку, по вертикали и горизонтали и ее положение. Если решений несколько, выведите любое.
\(1 \leq n, m \leq 300\). Решение оценивается в \(50\) баллов.
Дополнительные ограничения отсутствуют. Решение оценивается в \(50\) баллов.