Задача №115194. Параллельные вселенные
Берляндия — страна с очень развитой дорожной системой. Всего в Берляндии есть \(n\) городов, при том между каждой парой городов есть ровно одна дорога, доступная для движения в обе стороны.
В целях экономии электричества, в Берляндии освещены лишь \(m_1\) дорог, \(i\)-я из них соединяет города \(v_i\) и \(u_i\). Из соображений безопасности в Берляндии запрещено перемещаться по неосвещённым дорогам.
В параллельной вселенной есть аналогичная страна Черляндия, состоящая из \(n\) городов. В ней также между каждой парой городов есть ровно одна дорога. Страны отличаются только экономией электричества: в Черляндии освещены \(m_2\) дорог, \(i\)-я из них соединяет города \(a_i\) и \(b_i\). Известно, что в Черляндии можно доехать от любого города до любого, используя только освещённые дороги.
Вы владеете секретным заклинанием, позволяющим выбрать любые два различных города \(x\) и \(y\) и изменить освещённость на дороге между городами \(x\) и \(y\) в обеих вселенных. То есть в каждой из вселенных если дорога не была освещена, то она становится освещённой и наоборот.
Вы хотите использовать это заклинание не больше чем \(n\) раз так, чтобы в Берляндии можно было доехать от любого города до любого другого, используя только освещённые дороги. При этом после применения каждого заклинания Черляндия должна оставаться связной , то есть не должно существовать двух городов, между которыми нельзя проехать по освещённым дорогам.
Определите, можно ли этого достигнуть, и если да, то найдите подходящую последовательность заклинаний.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находятся два целых числа \(t\) и \(g\) (\(1 \le t \le 60\,000\), \(0 \le g \le 10\)) — количество наборов входных данных и номер группы тестов. Далее следуют описания наборов входных данных.
В первой строке описания каждого набора входных данных находятся три целых числа \(n\), \(m_1\) и \(m_2\) (\(3 \le n \le 300\,000\), \(0 \le m_1, m_2 \le 300\,000\), \(m_1, m_2 \le \frac{n(n-1)}{2}\)) — количество городов, количество освещённых дорог в Берляндии и количество освещённых дорог в Черляндии.
В следующих \(m_1\) строках содержатся описания освещённых дорог в Берляндии. В \(i\)-й строке находятся два целых числа \(v_i\) и \(u_i\) (\(1 \le v_i, u_i \le n\)) — номера городов, соединённых \(i\)-й освещенной дорогой. Гарантируется, что все дороги различны.
В следующих \(m_2\) строках содержатся описания освещённых дорог в Черляндии. В \(i\)-й строке находятся два целых числа \(a_i\) и \(b_i\) (\(1 \le a_i, b_i \le n\)) — номера городов, соединённых \(i\)-й освещенной дорогой. Гарантируется, что все дороги различны, и что в Черляндии между любыми двумя городами существует путь, проходящий только по освещенным дорогам.
Обозначим за \(N\), \(M_1\) и \(M_2\) сумму \(n\), \(m_1\) и \(m_2\) по всем наборам входных данных в одном тесте. Гарантируется, что \(N, M_1, M_2 \le 300\,000\).
Для каждого набора входных данных выведите « No » (без кавычек), если не существует последовательности заклинаний, удовлетворяющей всем условиям.
В противном случае выведите « Yes ». Во второй строке выведите целое число \(k\) (\(0 \le k \le n\)) — количество использованных вами заклинаний.
Далее выведите \(k\) строк. В \(i\)-й из них выведите два целых числа \(x_i\) и \(y_i\) (\(1 \le x_i, y_i \le n\), \(x_i \neq y_i\)) — номера городов, к которым применяется \(i\)-е заклинание. Обратите внимание, что после применения каждого заклинания Черляндия должна оставаться связной .
В первом наборе входных данных не существует ни одной подходящей последовательности заклинаний, поэтому ответ « No ».
Во втором наборе входных данных освещённые дороги изначально имеют такую структуру:
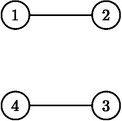
Берляндия
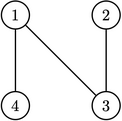
Черляндия
После применения заклинания к городам \(2\) и \(4\) и в Берляндии, и в Черляндии эта дорога становится освещённой, так как в обоих странах она была неосвещена. После этого, страны будут иметь следующую структуру:
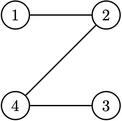
Берляндия
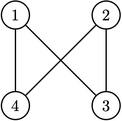
Черляндия
После этой операции, в Берляндии можно доехать от любого города до другого, поэтому такая последовательность заклинания корректна.
В третьем наборе входных данных, после применения заклинания к городам \(1\) и \(2\), в Берляндии дорога между этими двумя городами перестаёт быть освещённой, так как до этого она была освещена. В Черляндии наоборот — дорога становится освещённой. После этого, страны будут иметь следующую структуру структуру:
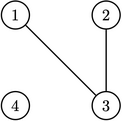
Берляндия
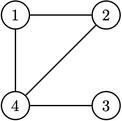
Черляндия
После применения заклинания к городам \(2\) и \(4\), страны будут иметь следующую структуру:
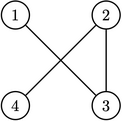
Берляндия
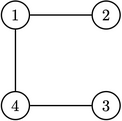
Черляндия
Тесты к этой задаче состоят из десяти групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, прохождение тестов из условия не требуется для некоторых групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
| Доп. ограничения | ||||
| Группа | Баллы | \(N, M_1, M_2\) | Необх. группы | Комментарий |
| 0 | 0 | – | – | Тесты из условия. |
| 1 | 9 | \(N, M_1, M_2 \le 3000\) | – | \(n \le 5\) |
| 2 | 7 | \(N, M_1, M_2 \le 3000\) | – | \(m_2 = \frac{n(n - 1)}{2}\) |
| 3 | 10 | \(N, M_1, M_2 \le 3000\) | – | |
| 4 | 11 | \(N, M_1, M_2 \le 3000\) | – | |
| 5 | 15 | \(N, M_1, M_2 \le 3000\) | – | |
| 6 | 8 | \(N, M_1, M_2 \le 3000\) | 5 | \(m_2 = n - 1\) |
| 7 | 12 | \(N, M_1, M_2 \le 3000\) | – | |
| 8 | 6 | \(N, M_1, M_2 \le 3000\) | 0 – 7 | |
| 9 | 8 | – | – | |
| 10 | 14 | – | 0 – 9 | Offline-проверка. |
\(^1\) Компонента связности — это множество городов, что между каждой парой из них можно доехать от одного до другого, используя только освещённые дороги.
\(^2\) Город называется изолированным , если не существует освещённой дороги, соединяющей этот город с каким-то другим.
3 0 3 0 3 1 2 2 3 1 3 4 2 3 1 2 3 4 1 3 1 4 2 3 4 3 3 1 2 2 3 1 3 1 4 2 4 3 4
No Yes 1 2 4 Yes 2 1 2 4 2