Дано прямоугольное шахматное поле размером n × m клеток (n столбцов, m строк), на котором находятся два короля. Для каждого короля даны его начальные координаты (x, y) и начальный вектор скорости (vx, vy). Числа vx и vy обозначают, что за один ход фигура передвигается на vx клеток по горизонтали и на vy по верткали, при этом числа vx и vy могут принимать значения - 1, 0 и 1. Короли по очереди делают ходы в направлении своих векторов скоростей, меняя направления у стенок доски по закону отражения (при отражении от края доски одна из компонент скорости меняется, при отражении от угла меняются обе компоненты скорости). Если король после очередного хода попадает на клетку с королём противника, то он объявляется победителем и игра заканчивается. Первым ходит белый король.
Требуется определить, закончится ли игра и, в случае положительного ответа, кто из королей и на каком ходу выиграет.
В первой строке входного файла даны натуральные числа n и m (1 ≤ n, m ≤ 106). Во второй строке находятся четыре целых числа xw, yw, vx, w, vy, w, задающие начальное положение и вестор скорости белого короля. В третьей строке даны четыре целых числа, xb, yb, vx, b, vy, b, задающие начальное положение и вектор скорости чёрного короля. Гарантируется, что 1 ≤ xw, xb ≤ n, 1 ≤ yw, yb ≤ m, - 1 ≤ vx, w, vy, w, vx, b, vy, b ≤ 1. Кроме того, гарантируется, что короли не могут иметь нулевой вектор скорости (обе компоненты не могут быть одноременно равны 0).
В случае, если игра не закончится, в выходной файл следует выдать единственную строку «TIE». Если же игра закончится после k-го хода одного из королей, программа должна выдать строку, содержащую «WHITE k» или «BLACK k».
Решения, корректно работающие при 1 ≤ n, m ≤ 50, будут набирать не менее 20 баллов. Решения, корректно работающие при 1 ≤ n, m ≤ 1000, будут набирать не менее 50 баллов.
3 3 1 2 1 1 2 1 1 1
WHITE 2
3 3 1 1 1 1 3 1 1 1
BLACK 1
Картина в голове Штирлица не складывалась. За год из Центра поступило N · M фрагментов нового задания. Штирлиц запомнил каждый фрагмент и теперь складывает из них целое сообщение.
Текст задания записан на клетчатой прямоугольной странице размера (5N) × (5M), который разрезан на N · M частей. Каждый фрагмент сообщения можно представить квадратом 5 × 5 (серые клетки), у которого с каждого краю (заштрихованные области) может быть только один «выступ» или «впадина». Обратите внимание, что к краям не относятся углы квадрата (см. иллюстрацию).
Более формально, каждый фрагмент можно представить в виде фигуры, которая получена из левой части иллюстрации, изменением цвета не более чем одной клетки из каждой заштрихованной области.
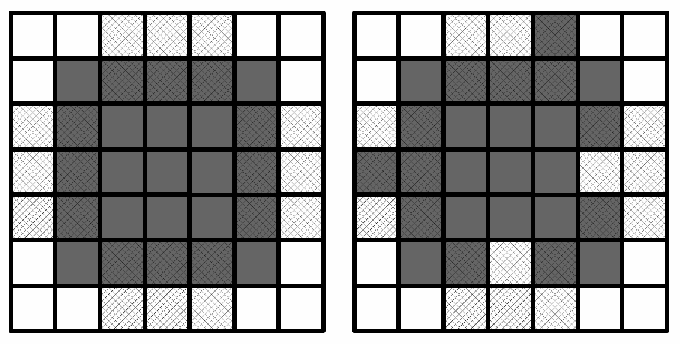
Фрагмент может иметь ровную сторону (т.е. не имеет выступа или впадины) только если соответствующая сторона фрагмента является границей сообщения.
Требуется написать программу, которая поможет Штирлицу собрать из фрагментов целое сообщение.
В первой строке входных данных даются размеры сообщения — натуральные числа N и M (1 ≤ N ≤ 5, 1 ≤ M ≤ 4).
В следующих 7 · N · M строках по 7 символов задаются фрагменты сообщения. Каждый фрагмент состоит из 7 строк. Пустая часть фрагмента задается символами «.», а часть фрагмента, содержащая текст, символами «#».
Выведите 7 · N строк по 7 · M символов, задающих как надо разложить части, чтобы получить целое сообщение. Части сообщения можно совмещать только параллельным переносом (то есть, запрещается поворачивать и переворачивать фрагменты сообщения).
Если существует несколько способов восстановить сообщение, требуется вывести любой из них. Решения, корректно работающие при ограничениях N · M ≤ 10, оцениваются в 50 баллов.
1 2 ....... .#####. .#####. .####.. .#####. .#####. ....... ....... .#####. .#####. ######. .#####. .#####. .......
.............. .#####..#####. .#####..#####. .####..######. .#####..#####. .#####..#####. ..............
Уран наконец-то освоен! МОЗГу удалось и на этой мертвой планете поставить нужные преобразователи. Теперь на этой планете можно проводить некоторое время без вреда для здоровья. Чем и решили воспользоваться межпланетные туристические фирмы. Одна из них - «С нами хоть на Луну» - решила потратить весь свой фонд на покупку квадратных участков на Уране. Дабы не потерять в прибыли — нужно потратить весь фонд до монеты, а чтобы иметь меньше проблем с Межпланетной налогово-таможенной службой, было бы здорово купить наименьшее количество участков. Цена 1 кв.м. планеты - 1 монета.
Помогите решить проблему турфирмы.
В единственной строке задано одно число — количество монет в фонде турфирмы. Количество монет не превышает 100.
Выведите минимальное количество квадратных участков, которое можно купить, потратив все деньги.
15
4
МОЗГ организация авторитетная. Ей поручают очень важные разработки. В данный момент многие из планетарных союзов в галактике заказывают разработку сторожевого силового щита вокруг их планет. И первой задачей при постройке такого щита является заказ ультраплотной плазмы. Ультраплазма невероятно дорога, поэтому заказывать с запасом — дорогого стоит.
Представим себе планеты как окружности с некоторым одинаковым радиусом, тогда щит нужно построить так:
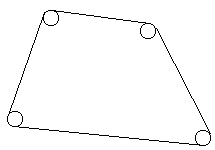
Вам дано количество планет в союзе, радиус для всех планет. Необходимо определить длину сечения сторожевого щита, это поможет оформить заказ на плазму с минимальными тратами.
В первой строке находятся два числа — количество гвоздей \(N\), \(1 \leq N \leq \)100, и вещественное число \(R\) — радиус планет.
Далее на входе располагаются еще \(N\) строк, в каждой из которых записана через пробел пара вещественных координат очередной планеты; координаты не превосходят по абсолютной величине числа 100. Описания планет приводятся в порядке обхода вершин многоугольника (либо по часовой стрелке, либо против часовой стрелки), начиная с произвольного.
Выведите вещественное число, округлённое до двух знаков после запятой — длину сечения щита.
4 1 0.0 0.0 2.0 0.0 2.0 2.0 0.0 2.0
14.28
Ученые из МОЗГ очень интересуются возможностями одноименного органа. Они очень близки к прорыву. Один из добровольцев уже в течении недели принимает препарат, которые позволяет ему читать мысли другого человека. И сегодня первый день серьезных испытаний.
Компьютер выдаст на монитор одному из участников проекта до \(10^5\) целых чисел, которые нужно прочесть про себя. В этот же момент доброволец будет пытаться считать эти числа у первого из головы, а потом записать до \(10^3\) чисел, которые запомнил.
Вам необходимо узнать результаты теста, чтобы продолжать испытания. Необходимо ответить на вопрос, сколько чисел из начального набора угадал испытуемый.
В первой строке целые числа \(N\) (\(1 \leq N \leq 10^5\)) и \(M\) (\(1 \leq M \leq 10^3\)) — количество исходных и угаданных чисел соответственно.
Во второй строке \(N\) чисел — исходный набор различных, отсортированный в порядке возрастания.
В третьей строке \(M\) чисел — предположения добровольца о числах.
Выведите количество угаданных чисел.
10 5 1 2 3 4 5 6 7 8 9 10 3 1 5 11 7
4
10 10 1 2 3 4 5 11 12 13 14 15 20 21 22 23 24 25 26 27 28 29
0